如图，在梯形 $ ABCD $ 中，$ AB\parallel CD$，$E$，$F $ 是线段 $ AB $ 上的两点，且 $ DE\perp AB$，$CF\perp AB$，$AB=12 $，$ AD=5,BC=4{\sqrt{2}}$，$DE=4 $．现将 $ \triangle ADE$，$\triangle CFB $ 分别沿 $ DE$，$CF $ 折起，使 $ A$，$B $ 两点重合于点 $ G $，得到多面体 $ CDEFG $．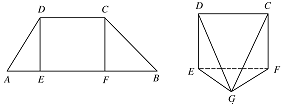
【难度】
【出处】
2012年高考江西卷（文）
【标注】
-
求证：平面 $ DEG\perp $ 平面 $ CFG $；标注答案略解析因为 $ DE\perp EF $，$CF\perp EF$，所以四边形 $ CDEF $ 为矩形，
由 $ GD=5$，$DE=4 $，得\[ GE={\sqrt{GD^2-DE^2}}=3, \]由 $ GC=4{\sqrt{2}}$，$CF=4 $，得\[ FG={\sqrt{GC^2-CF^2}}=4, \]所以\[ EF=5.\]在 $ \triangle EFG $ 中，有 $ EF^2=GE^2+FG^2 $，所以 $ EG\perp GF $．
又因为 $ CF\perp EF$，$CF\perp FG $，得 $ CF\perp $ 平面 $ EFG $，
所以 $ CF\perp EG $，所以 $ EG\perp $ 平面 $ CFG $，所以平面 $ DEG\perp $ 平面 $ CFG $． -
求多面体 $ CDEFG $ 的体积．标注答案略解析如图，在平面 $ EGF $ 中，过点 $ G $ 作 $ GH\perp EF $ 于点 $ H $．
则\[ GH={\dfrac{EG\cdot GF}{EF}}={\dfrac{12}{5}}. \]因为平面 $ CDEF\perp $ 平面 $ EFG $，得 $ GH\perp $ 平面 $ CDEF $，\[ V_{CDEFG}={\dfrac{1}{3}}S_{四边形CDEF}\cdot GH=16. \]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
