如图，直三棱柱 $ ABC-A′B′C′$，$\angle BAC=90^\circ$，$AB=AC={\sqrt{2}}$，$AA′=1 $，点 $ M$、$N $ 分别为 $ A′B $ 和 $ B′C′ $ 的中点．（锥体体积公式 $ V={\dfrac{1}{3}}Sh $，其中 $ S $ 为底面面积，$ h $ 为高）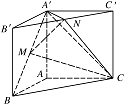
【难度】
【出处】
2012年高考辽宁卷（文）
【标注】
-
证明：$ MN\parallel 平面 A′ACC′ $；标注答案略解析证法一：连接 $ AB′$，$AC′ $，由已知 $ \angle BAC=90^\circ$，$AB=AC $，
三棱柱 $ ABC-A′B′C′ $ 为直三棱柱，所以 $ M $ 为 $ AB′ $ 中点．
又因为 $ N $ 为 $ B′C′ $ 的中点，所以 $ MN\parallel AC′ $．
又 $ MN \not\subset 平面 A′ACC′ $，$ AC′ \subset 平面 A′ACC′ $，
因此 $ MN\parallel 平面 A′ACC′ $．
证法二：取 $ A′B′ $ 中点 $ P $，连接 $ MP$，$NP $．
因为 $ M$，$N $ 分别为 $ AB′ $ 与 $ B′C′ $ 的中点，
所以 $ MP\parallel AA′$，$PN\parallel A′C′ $，
所以 $ MP\parallel 平面 A′ACC′ $，$ PN\parallel 平面 A′ACC′ $，
又 $ MP\cap NP=P $，因此平面 $ MPN\parallel 平面 A′ACC′ $，
而 $ MN \subset 平面 MPN $．因此 $ MN\parallel 平面 A′ACC′ $． -
求三棱锥 $ A′-MNC $ 的体积．标注答案$ \dfrac{1}{6} $解析解法一：连接 $ BN $，如图，
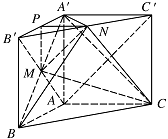由题意得 $ A′N\perp B′C′ $，$ A′N\perp B′B $，
所以 $ A′N\perp 平面 NBC $．
又 $ A′N={\dfrac{1}{2}}B′C′=1 $，故\[\begin{split} V_{A′-MNC}&=V_{N-A′MC}\\&=\dfrac{1}{2}V_{N-A′BC}\\&=\dfrac{1}{2}V_{A′-NBC}=\dfrac{1}{6}.\end{split}\]解法二：\[\begin{split} V_{A′-MNC}&=V_{A′-NBC}-V_{M-NBC}\\&=\dfrac{1}{2}V_{A′-NBC}=\dfrac{1}{6}. \end{split}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
