如图,动圆 $ C_1:x^2+y^2=t^2$,$1<t<3 $,与椭圆 $ C_2:{\dfrac{x^2}{9}}+y^2=1 $ 相交于 $ A$,$B$,$C$,$D $ 四点,点 $ A_1$,$A_2 $ 分别为 $ C_2 $ 的左、右顶点.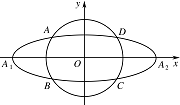

【难度】
【出处】
2012年高考辽宁卷(文)
【标注】
-
当 $ t $ 为何值时,矩形 $ ABCD $ 的面积取得最大值?并求出其最大面积;标注答案略解析设 $ A\left(x_0,y_0\right) $,则矩形 $ ABCD $ 的面积 $ S=4|x_0||y_0| $.由 $ \dfrac{x^2_0}{9}+y^2_0=1 $ 得\[ y^2_0=1-\dfrac{x^2_0}{9}, \]从而\[ \begin{split}x^2_0y^2_0&=x^2_0 \left(1-\dfrac{x^2_0}{9} \right)\\&=-\dfrac{1}{9}\left(x^2_0-\dfrac{9}{2}\right)^ 2+\dfrac{9}{4}.\end{split}\]当 $ x^2_0=\dfrac{9}{2}$,$y^2_0=\dfrac{1}{2} $ 时,\[ S_{\max}=6. \]从而 $ t=\sqrt{5} $ 时,矩形 $ ABCD $ 的面积最大,最大面积为 $ 6 $.
-
求直线 $ AA_1 $ 与直线 $ A_2B $ 交点 $ M $ 的轨迹方程.标注答案略解析由 $ A\left(x_0,y_0\right)$,$B\left(x_0,-y_0\right)$,$A_1\left(-3,0\right)$,$A_2\left(3,0\right) $ 知直线 $ AA_1 $ 的方程为\[ y={\dfrac{y_0}{x_0+3}}\left(x+3\right) ,\quad \cdots \cdots ① \]直线 $ A_2B $ 的方程为\[ y={\dfrac{-y_0}{x_0-3}}\left(x-3\right) ,\quad \cdots \cdots ② \]由 ①② 得\[ y^2={\dfrac{-y^2_0}{x^2_0-9}}\left(x^2-9\right), \quad \cdots \cdots ③ \]又点 $ A\left(x_0,y_0\right) $ 在椭圆 $ C $ 上,故\[ y^2_0=1-{\dfrac{x^2_0}{9}}, \quad \cdots \cdots ④ \]将 ④ 代入 ③ 得\[ {\dfrac{x^2}{9}}-y^2=1\left(x<-3,y<0\right).\]因此点 $ M $ 的轨迹方程为\[ {\dfrac{x^2}{9}}-y^2=1\left(x<-3,y<0\right).\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2