已知 $x_1\ln x_1=x_2\ln x_2=a$（$x_1< x_2$），${\rm e}$ 是自然对数的底．求证：$x_2-x_1<2a+1+{\rm e}^{-2}$．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
设函数 $f(x)=x\ln x$，则其导函数\[f'(x)=1+\ln x.\]取其在 $x={\rm e}^{-2}$ 和 $x=1$ 处的切线，分别为 $l_1:y=-x-{\rm e}^{-2}$ 和 $l_2:y=x-1$，如图．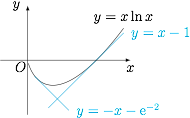
直线 $y=a$ 与直线 $l_1$，函数 $f(x)$ 的图象和直线 $l_2$ 分别交于 $x_1',x_1,x_2,x_2'$，则有\[x_1'<x_1<x_2<x_2',\]因此有\[x_2-x_1<x_2'-x_1'=(a+1)-(-a-{\rm e}^{-2})=2a+1+{\rm e}^{-2}.\]
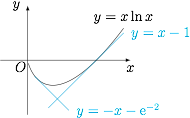直线 $y=a$ 与直线 $l_1$，函数 $f(x)$ 的图象和直线 $l_2$ 分别交于 $x_1',x_1,x_2,x_2'$，则有\[x_1'<x_1<x_2<x_2',\]因此有\[x_2-x_1<x_2'-x_1'=(a+1)-(-a-{\rm e}^{-2})=2a+1+{\rm e}^{-2}.\]
答案
解析
备注
