定义在 $\mathbb R$ 上的奇函数 $f(x)$ 满足 $f(2+x)=f(2-x)$，当 $x\in [0,2]$ 时，$f(x)=-4x^2+8x$．若在区间 $[a,b]$ 上，存在 $m$（$m\geqslant 3$）个不同的整数 $x_i$（$i=1,2,\cdots,m$）满足 $\displaystyle \sum_{i=1}^{m-1}{\left|f(x_i)-f(x_{i+1})\right|}\geqslant 72$，求 $b-a$ 的最小值．
【难度】
【出处】
无
【标注】
【答案】
$16$
【解析】
函数 $f(x)$ 的图象在一个周期内的图象如图．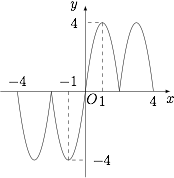
为了使得 $S=\displaystyle \sum_{i=1}^{m-1}{\left|f(x_i)-f(x_{i+1)})\right|}$ 尽可能大，应该让相邻的函数值 $f(x_i)$ 尽可能交替取 $4$ 和 $-4$，因此取\[x_i:1,-1,3,-3,5,-5,7,-7,9,-9.\]注意到在序列最前和最后各增加一个函数值为 $0$ 的整点（加在序列中对求和没有贡献）可以获得额外的 $S$，于是取\[x_i:0,1,-1,3,-3,5,-5,7,-7,9,2\]就得到了 $S=72$．此时 $x_i\in [-7,9]$（$i=1,2,\cdots,m$），这样就得到了 $b-a=16$ 的例子．
接下来证明 $b-a$ 不能取得比 $16$ 更小的值．若 $b-a<16$，则区间 $[a,b]$ 内函数值为 $\pm 4$ 的整数 $x$ 不超过 $8$ 个，显然此时\[S\leqslant 4+7\times 8+4=64,\]不符合题意．
综上所述，$b-a$ 的最小值为 $16$．
为了使得 $S=\displaystyle \sum_{i=1}^{m-1}{\left|f(x_i)-f(x_{i+1)})\right|}$ 尽可能大，应该让相邻的函数值 $f(x_i)$ 尽可能交替取 $4$ 和 $-4$，因此取\[x_i:1,-1,3,-3,5,-5,7,-7,9,-9.\]注意到在序列最前和最后各增加一个函数值为 $0$ 的整点（加在序列中对求和没有贡献）可以获得额外的 $S$，于是取\[x_i:0,1,-1,3,-3,5,-5,7,-7,9,2\]就得到了 $S=72$．此时 $x_i\in [-7,9]$（$i=1,2,\cdots,m$），这样就得到了 $b-a=16$ 的例子．接下来证明 $b-a$ 不能取得比 $16$ 更小的值．若 $b-a<16$，则区间 $[a,b]$ 内函数值为 $\pm 4$ 的整数 $x$ 不超过 $8$ 个，显然此时\[S\leqslant 4+7\times 8+4=64,\]不符合题意．
综上所述，$b-a$ 的最小值为 $16$．
答案
解析
备注
