已知 $A$ 是椭圆 $E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)的右顶点,过 $A$ 作互相垂直的两条直线 $AP$ 和 $AQ$ 分别交椭圆于 $P,Q$.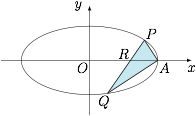

【难度】
【出处】
无
【标注】
-
求证:直线 $PQ$ 过定点 $R$,并求出定点 $R$ 的坐标;标注答案$\left(\dfrac{a^2-b^2}{a^2+b^2}\cdot a,0\right)$解析将坐标系平移至以 $A$ 为新坐标原点,则$$E':\dfrac{x'^2}{a^2}+\dfrac{y'^2}{b^2}+\dfrac{2}{a}x'=0.$$设新坐标系下直线 $P'Q'$ 的方程为 $mx'+ny'=1$,化齐次联立可得\[\dfrac{x'^2}{a^2}+\dfrac{y'^2}{b^2}+\dfrac 2ax'(mx'+ny')=0.\]由于 $AP\perp AQ$,于是\[\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{2m}a=0,\]于是 $m$ 为定值,直线 $P'Q'$ 恒过定点 $R'\left(\dfrac 1m,0\right)$,即 $R'\left(-\dfrac{2ab}{a^2+b^2}\cdot b,0\right)$.因此在原坐标系下对应的 $R$ 点坐标为\[\left(\dfrac{a^2-b^2}{a^2+b^2}\cdot a,0\right).\]
-
求 $\triangle APQ$ 面积的最大值.标注答案$\begin{cases}\dfrac{ab^3}{a^2-b^2},&\dfrac ab\geqslant \sqrt 2+1,\\ \dfrac{4a^2b^4}{(a^2+b^2)^2},&\dfrac ab<\sqrt 2+1. \end{cases}$解析考虑到 $R$ 点为定点,于是\[\dfrac{S_{\triangle APQ}}{S_{\triangle OPQ}}=\dfrac{AR}{OR}=\dfrac{2b^2}{a^2-b^2}.\]接下来计算 $\triangle OPQ$ 面积的最大值.
在仿射变换 $x'=x$,$y'=\dfrac aby$ 下,椭圆 $E$ 变为圆$$E':x'^2+y'^2=a^2.$$设 $O$ 到直线 $P'Q'$ 的距离为 $d$,则 $d$ 的取值范围为 $(0,OR]$ 即 $\left(0,\dfrac{a^2-b^2}{a^2+b^2}\cdot a\right]$,此时 $\triangle OP'Q'$ 的面积\[S=\dfrac 12\cdot d\cdot 2\sqrt{a^2-d^2}=\sqrt{d^2(a^2-d^2)}.\]情形一 $\dfrac{a^2-b^2}{a^2+b^2}\geqslant \dfrac{1}{\sqrt 2}$,即 $\dfrac ab\geqslant \sqrt 2+1$ 时,$S$ 的最大值当 $d^2=\dfrac {a^2}2$ 时取得,为 $\dfrac{a^2}2$.
此时 $\triangle OPQ$ 的面积的最大值为$$\dfrac ba\cdot \dfrac{a^2}2=\dfrac 12ab,$$进而对应 $\triangle APQ$ 面积的最大值为\[\dfrac 12ab\cdot \dfrac{2b^2}{a^2-b^2}= \dfrac{ab^3}{a^2-b^2}.\]情形二 $\dfrac{a^2-b^2}{a^2+b^2}< \dfrac{1}{\sqrt 2}$,即 $\dfrac ab<\sqrt 2+1$ 时,$S$ 的最大值当 $d=\dfrac{a^2-b^2}{a^2+b^2}\cdot a$ 时取得,为\[\dfrac{a^2-b^2}{a^2+b^2}\cdot a\cdot \sqrt{a^2-\left(\dfrac{a^2-b^2}{a^2+b^2}\right)^2\cdot a^2}=\dfrac{2a^3b(a^2-b^2)}{(a^2+b^2)^2}.\]此时 $\triangle OPQ$ 的面积的最大值为\[\dfrac ba\cdot \dfrac{2a^3b(a^2-b^2)}{(a^2+b^2)^2}=\dfrac{2a^2b^2(a^2-b^2)}{(a^2+b^2)^2},\]进而对应 $\triangle APQ$ 面积的最大值为\[\dfrac{2a^2b^2(a^2-b^2)}{(a^2+b^2)^2}\cdot \dfrac{2b^2}{a^2-b^2}=\dfrac{4a^2b^4}{(a^2+b^2)^2}.\]综上所述,$\triangle APQ$ 面积的最大值为\[\begin{cases}\dfrac{ab^3}{a^2-b^2},&\dfrac ab\geqslant \sqrt 2+1,\\ \dfrac{4a^2b^4}{(a^2+b^2)^2},&\dfrac ab<\sqrt 2+1. \end{cases}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2