设函数 $f(x)=-x^2+bx+|x-a|$，$a,b\in\mathbb R$，若对任意的实数 $a$，关于 $x$ 的方程 $f(x)=a+1$ 至多有两个不同的解，求实数 $b$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$\left(-\infty,1-2\sqrt 2\right]\cup (-1,3)\cup \left[1+2\sqrt 2,+\infty\right)$
【解析】
函数 $f(x)$ 即\[f(x)=\begin{cases}-x^2+(b-1)x+a,&x<a,\\ -x^2+(b+1)x-a,&x\geqslant a.\end{cases}\]考虑问题的反面，存在实数 $a$，使得方程 $f(x)=a+1$ 有至少 $3$ 个解，求实数 $b$ 的取值范围．
情形一 当 $a\notin \left(\dfrac{b-1}2,\dfrac{b+1}2\right)$ 时，函数 $f(x)$ 先单调递增后单调递减，至多有 $2$ 个实数解；
情形二 当 $a\in \left(\dfrac{b-1}2,\dfrac{b+1}2\right)$ 时，函数的图象为形如“m”，此时只要\[f(a)\leqslant a+1\leqslant \min\left\{f\left(\dfrac{b-1}2\right),f\left(\dfrac{b+1}2\right)\right\},\]即\[-a^2+ab\leqslant a+1\leqslant \min\left\{a+\dfrac 14(b-1)^2,-a+\dfrac 14(b+1)^2\right\}.\]利用规划处理，不等式组为\[\begin{cases}\dfrac 12b-\dfrac 12<a<\dfrac 12b+\dfrac 12,\\ b\leqslant -1\lor b\geqslant 3,\\ a\leqslant \dfrac 18(b+1)^2-\dfrac 12,\end{cases}\]因为当 $a>0$ 时，$$b\leqslant a+\dfrac 1a+1,$$当 $a<0$ 时，$$b\geqslant a+\dfrac 1a+1,$$所以点 $(b,a)$ 在双曲线 $x=y+\dfrac 1y+1$ 外部，如图．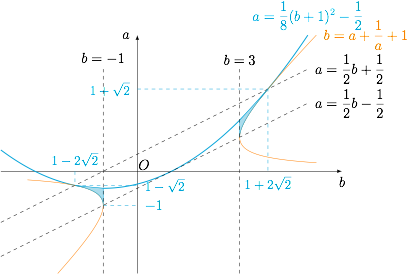
因此 $b$ 的取值范围是 $\left(1-2\sqrt 2,-1\right]\cup \left[3,1+2\sqrt 2\right)$．
回到原题，所求的取值范围是 $\left(-\infty,1-2\sqrt 2\right]\cup (-1,3)\cup \left[1+2\sqrt 2,+\infty\right)$．
因此 $b$ 的取值范围是 $\left(1-2\sqrt 2,-1\right]\cup \left[3,1+2\sqrt 2\right)$．回到原题，所求的取值范围是 $\left(-\infty,1-2\sqrt 2\right]\cup (-1,3)\cup \left[1+2\sqrt 2,+\infty\right)$．
答案
解析
备注
