已知边长为 $1$ 的正三角形的中心为 $O$，过 $O$ 的直线与边 $AB,AC$ 分别交于点 $M,N$，求 $\dfrac{1}{OM^2}+\dfrac{1}{ON^2}$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$[15,18]$
【解析】
如图．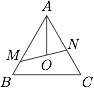
注意到$$\angle AMO+\angle ANO=\dfrac{2\pi}3$$为定值，设 $\angle AMO=\dfrac{\pi}3+x$，$\angle ANO=\dfrac{\pi}3-x$，其中 $x$ 的取值范围是 $\left[-\dfrac{\pi}6,\dfrac{\pi}6\right]$．
在 $\triangle AMO$ 和 $\triangle ANO$ 中分别应用正弦定理，可得\[\begin{aligned} \dfrac{OA}{\sin\left(\dfrac{\pi}3+x\right)}=\dfrac{OM}{\sin\dfrac{\pi}6},\\ \dfrac{OA}{\sin\left(\dfrac{\pi}3-x\right)}=\dfrac{ON}{\sin\dfrac{\pi}6},\end{aligned}\]这样就有\[\begin{split}\dfrac{1}{OM^2}+\dfrac{1}{ON^2}&=\dfrac{\sin^2\left(\dfrac{\pi}3+x\right)+\sin^2\left(\dfrac{\pi}3-x\right)}{\sin^2\dfrac{\pi}6\cdot OA^2}\\
&=12\left[\left(\dfrac{\sqrt 3}2\cos x+\dfrac 12\sin x\right)^2+\left(\dfrac{\sqrt 3}2\cos x-\dfrac 12\sin x\right)^2\right]\\
&=12\left(\dfrac 32\cos^2x+\dfrac 12\sin^2x\right)\\
&=12\left(\dfrac 12+\cos^2x\right),
\end{split}\]考虑到 $\cos^2x$ 的取值范围是 $\left[\dfrac 34,1\right]$，因此所求的取值范围是 $[15,18]$．
注意到$$\angle AMO+\angle ANO=\dfrac{2\pi}3$$为定值，设 $\angle AMO=\dfrac{\pi}3+x$，$\angle ANO=\dfrac{\pi}3-x$，其中 $x$ 的取值范围是 $\left[-\dfrac{\pi}6,\dfrac{\pi}6\right]$．在 $\triangle AMO$ 和 $\triangle ANO$ 中分别应用正弦定理，可得\[\begin{aligned} \dfrac{OA}{\sin\left(\dfrac{\pi}3+x\right)}=\dfrac{OM}{\sin\dfrac{\pi}6},\\ \dfrac{OA}{\sin\left(\dfrac{\pi}3-x\right)}=\dfrac{ON}{\sin\dfrac{\pi}6},\end{aligned}\]这样就有\[\begin{split}\dfrac{1}{OM^2}+\dfrac{1}{ON^2}&=\dfrac{\sin^2\left(\dfrac{\pi}3+x\right)+\sin^2\left(\dfrac{\pi}3-x\right)}{\sin^2\dfrac{\pi}6\cdot OA^2}\\
&=12\left[\left(\dfrac{\sqrt 3}2\cos x+\dfrac 12\sin x\right)^2+\left(\dfrac{\sqrt 3}2\cos x-\dfrac 12\sin x\right)^2\right]\\
&=12\left(\dfrac 32\cos^2x+\dfrac 12\sin^2x\right)\\
&=12\left(\dfrac 12+\cos^2x\right),
\end{split}\]考虑到 $\cos^2x$ 的取值范围是 $\left[\dfrac 34,1\right]$，因此所求的取值范围是 $[15,18]$．
答案
解析
备注
