在正八棱锥中，相邻两个侧面所成的二面角的平面角记作 $\alpha$，那么 $\alpha$ 的取值范围是 \((\qquad)\)
【难度】
【出处】
2008年第十九届“希望杯”全国数学邀请赛高二（二试）
【标注】
【答案】
B
【解析】
如图，二面角角 $A-PB-C$ 为 $\alpha$，设 $\angle PBA=\theta_1$，$\angle PBC=\theta_2$，$\angle ABC=\varphi$．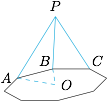
根据三射线定理，有$$\cos\varphi=\cos\theta_1\cos\theta_2+\sin\theta_1\sin\theta_2\cos\alpha,$$由正八棱锥可知 $\theta_1=\theta_2\in\left(\dfrac{3\pi}{8},\dfrac{\pi}{2}\right)$，$\varphi=\dfrac{3\pi}{4}$，故有$$\cos\alpha=1-\dfrac{2+\sqrt2}{2\sin^2\theta_1},$$解得 $\cos\alpha$ 的取值范围是 $\left(-1,-\dfrac{\sqrt2}{2}\right)$，因此 $ \alpha $ 的取值范围是 $ \left(\dfrac{3\pi}{4},\pi\right)$．
根据三射线定理，有$$\cos\varphi=\cos\theta_1\cos\theta_2+\sin\theta_1\sin\theta_2\cos\alpha,$$由正八棱锥可知 $\theta_1=\theta_2\in\left(\dfrac{3\pi}{8},\dfrac{\pi}{2}\right)$，$\varphi=\dfrac{3\pi}{4}$，故有$$\cos\alpha=1-\dfrac{2+\sqrt2}{2\sin^2\theta_1},$$解得 $\cos\alpha$ 的取值范围是 $\left(-1,-\dfrac{\sqrt2}{2}\right)$，因此 $ \alpha $ 的取值范围是 $ \left(\dfrac{3\pi}{4},\pi\right)$．
题目
答案
解析
备注
