已知抛物线 $y=\dfrac 14x^2$ 和 $y=-\dfrac{1}{16}x^2+5$ 所围成的封闭曲线如图所示，给定 $A(0,a)$，若在此时封闭曲线上恰有三对不同的点，满足每一对点关于点 $A$ 对称，求实数 $a$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$\left(\dfrac 52,4\right)$
【解析】
问题即将封闭曲线关于 $x$ 轴的镜像向上平移，使得原封闭曲线与变换后的曲线恰好有 $6$ 个不同的公共点，如图．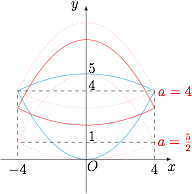
两个临界状态对应的 $a=\dfrac 52$ 和 $a=4$，于是实数 $a$ 的取值范围是 $\left(\dfrac 52,4\right)$．
两个临界状态对应的 $a=\dfrac 52$ 和 $a=4$，于是实数 $a$ 的取值范围是 $\left(\dfrac 52,4\right)$．
答案
解析
备注
