已知椭圆 $C_1:\dfrac{x^2}{a^2 }+\dfrac{y^2}{b^2 }=1\left(a>b>0\right) $ 的离心率为 $\dfrac{\sqrt{2}}{ 2} $,其短轴的下端点在抛物线 $x^2=4y $ 的准线上.设 $ O$ 为坐标原点,$ M$ 是直线 $l:x=2 $ 上的动点,$ F$ 为椭圆的右焦点,过点 $F $ 作 $OM $ 的垂线与以 $OM $ 为直径的圆 $C_2 $ 相交于 $P$,$Q $ 两点,与椭圆 $C_1 $ 相交于 $ A$,$B$ 两点,如图所示.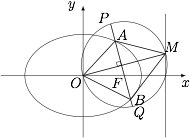

【难度】
【出处】
无
【标注】
-
求椭圆 $C_1 $ 的方程.标注答案$\dfrac{x^2}{2}+y^2=1$解析由题意得$$\begin{cases}\dfrac ca=\dfrac{\sqrt 2}{2},\\b=1,\end{cases}$$又 $a^2=b^2+c^2$,所以解得 $a=\sqrt 2$,$b=1$.
故椭圆方程为 $\dfrac{x^2}{2}+y^2=1$. -
若 $\left|PQ\right|=\sqrt{6} $,求圆 $C_2 $ 的方程;标注答案$(x-1)^2+(y\pm 1)^2=2$解析设 $OM$ 与 $PQ$ 交于 $E$ 点,$H(2,0)$.如图.
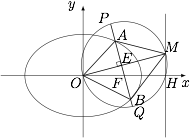 由于 $\triangle OEF$ 与 $\triangle OHM$ 相似,于是\[|OE|\cdot |OM|=|OF|\cdot |OH|=2,\]又根据相交弦定理,有\[|OE|\cdot |EM|=|PE|\cdot |EQ|=\dfrac 32,\]于是有$$|OE|\cdot|OE|=\dfrac 12,$$从而解得 $OM=2\sqrt 2$,因此 $M(2,\pm 2)$,进而可得圆 $C_2$ 的方程为\[(x-1)^2+(y\pm 1)^2=2.\]
由于 $\triangle OEF$ 与 $\triangle OHM$ 相似,于是\[|OE|\cdot |OM|=|OF|\cdot |OH|=2,\]又根据相交弦定理,有\[|OE|\cdot |EM|=|PE|\cdot |EQ|=\dfrac 32,\]于是有$$|OE|\cdot|OE|=\dfrac 12,$$从而解得 $OM=2\sqrt 2$,因此 $M(2,\pm 2)$,进而可得圆 $C_2$ 的方程为\[(x-1)^2+(y\pm 1)^2=2.\] -
设 $C_2 $ 与四边形 $OAMB $ 的面积分别为 $S_1,S_2 $,若 $S_1=\lambda S_2 $,求 $\lambda $ 的取值范围.标注答案$\left[\dfrac{\sqrt 2}2\pi,+\infty\right)$解析根据题意,有\[\lambda=\dfrac{S_1}{S_2}=\dfrac{\pi \cdot \left(\dfrac 12|OM|\right)^2}{\dfrac 12\cdot |AB|\cdot |OM|}=\dfrac{\pi}2\cdot \dfrac{|OM|}{|AB|},\]设直线 $PQ$ 的倾斜角为 $\theta$,则\[|AB|=\dfrac{2ab^2}{b^2+c^2\sin^2\theta}=\dfrac{2\sqrt 2}{1+\sin^2\theta},\]而\[|OM|=\dfrac{|OH|}{\sin\theta}=\dfrac{2}{\sin\theta},\]这样就有\[\lambda=\dfrac{\pi}2\cdot \dfrac{1+\sin^2\theta}{\sqrt 2\cdot \sin\theta}=\dfrac{\pi}{2\sqrt 2}\left(\sin\theta+\dfrac{1}{\sin\theta}\right),\]从而其取值范围是 $\left[\dfrac{\sqrt 2}2\pi,+\infty\right)$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3