在棱长为 $a$ 的正方体 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 中，$E$ 为棱 $AB$ 的中点．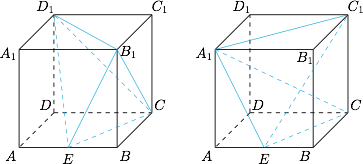
【难度】
【出处】
无
【标注】
-
求四面体 $E - {B_1}{D_1}C$ 的体积；标注答案$\dfrac{1}{4}{a^3}$解析过点 $E$ 作 $EG\parallel B_1D_1$，交 $CB$ 的延长线于 $G$，从而有$$V_{E-B_1D_1C}=V_{G-B_1D_1C}=V_{D_1-B_1CG}=\dfrac 13\cdot S_{\triangle B_1CG}\cdot a=\dfrac 13\cdot\dfrac 12\cdot\dfrac {3a}2\cdot a\cdot a=\dfrac 14a^3.$$如图．
-
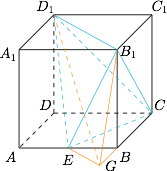
求点 $C$ 到平面 $EA_1C_1$ 的距离．标注答案$\dfrac 13a$解析连结 $AC$，因为 $AC\parallel A_1C_1$，所以点 $C$ 到平面 $EA_1C_1$ 的距离就等于点 $A$ 到平面 $EA_1C_1$ 的距离 $d$，如图．
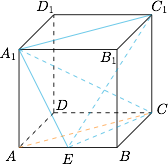考虑四面体 $A-A_1C_1E$ 的体积：$$V_{A-A_1EC_1}=\dfrac 13\cdot S_{\triangle A_1C_1E}\cdot d=V_{C_1-AEA_1}=\dfrac 13\cdot\dfrac 12\cdot \dfrac a2\cdot a\cdot a=\dfrac 1{12}a^3,$$而在 $\triangle A_1C_1E$ 中，有$$A_1C_1=\sqrt 2a,A_1E=\dfrac {\sqrt 5}2a,C_1E=\dfrac 32a,$$由余弦定理得 $\cos\angle EA_1C_1=\dfrac 1{\sqrt{10}}$，从而有$$S_{\triangle A_1C_1E}=\dfrac 12\cdot \sqrt 2a\cdot\dfrac{\sqrt 2}2a\cdot\dfrac{3}{\sqrt{10}}=\dfrac 34a^2,$$所以$$d=\dfrac{\dfrac{1}{12}a^3}{\dfrac 13\cdot\dfrac 34a^2}=\dfrac 13a.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
