在如图所示的几何体中,四边形 $ABCD$ 是等腰梯形,$AB\parallel CD$,$\angle DAB = {60^ \circ }$,$FC \perp 平面 ABCD$,$AE \perp BD$,$CB = CD = CF$.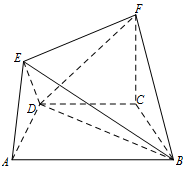

【难度】
【出处】
2012年高考山东卷(理)
【标注】
-
求证:$BD \perp 平面 AED$;标注答案略解析因为四边形 $ ABCD $ 是等腰梯形,$ AB\parallel CD $,$ \angle DAB=60^\circ $,
所以 $ \angle ADC=\angle BCD=120^\circ $.
又 $ CB=CD $,所以 $ \angle CDB=30^\circ $,
因此 $ \angle ADB=90^\circ $,$ AD\perp BD $,
又 $ AE\perp BD $,且 $ AE\cap AD=A $,$ AE , AD \subset平面 AED $,所以 $ BD\perp 平面 AED $. -
求二面角 $F - BD - C$ 的余弦值.标注答案略解析解法一:由(1)知 $ AD\perp BD $,所以 $ AC\perp BC $.
又 $ FC\perp 平面 ABCD $,因此 $ CA $,$ CB $,$ CF $ 两两垂直,
以 $ C $ 为坐标原点,分别以 $ CA $,$ CB $,$ CF $ 所在的直线为 $ x $ 轴,$ y $ 轴,$ z $ 轴,建立如图所示的空间直角坐标系.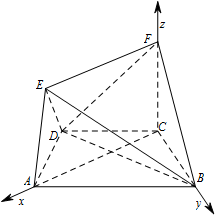 不妨设 $ CB=1 $,则 $ C\left(0,0,0\right) $,$ B\left(0,1,0\right) $,$ D\left( {\dfrac{{\sqrt{3}}}{2}},-{\dfrac{1}{2}},0 \right) $,$ F\left(0,0,1\right) $.
不妨设 $ CB=1 $,则 $ C\left(0,0,0\right) $,$ B\left(0,1,0\right) $,$ D\left( {\dfrac{{\sqrt{3}}}{2}},-{\dfrac{1}{2}},0 \right) $,$ F\left(0,0,1\right) $.
因此 $ {\overrightarrow {BD}}=\left( {\dfrac{{\sqrt{3}}}{2}},-{\dfrac{3}{2}},0 \right) $,$ {\overrightarrow {BF}}=\left(0,-1,1\right) $.
设平面 $ BDF $ 的法向量为 $ \overrightarrow m=\left(x,y,z\right) $,则 $ \overrightarrow m\cdot {\overrightarrow {BD}}=0 $,$\overrightarrow m\cdot {\overrightarrow {BF}}=0 $,
所以 $ x={\sqrt{3}}y={\sqrt{3}}z $,取 $ z=1 $,则 $ \overrightarrow m=\left({\sqrt{3}},1,1\right) $.
由于 $ {\overrightarrow {CF}}=\left(0,0,1\right) $ 是平面 $ BDC $ 的一个法向量,则\[ \cos \left\langle\overrightarrow m,{\overrightarrow {CF}} \right\rangle= \dfrac{\overrightarrow m\cdot {\overrightarrow {CF}} }{\left|\overrightarrow m \right| \left|{\overrightarrow {CF}} \right|} ={\dfrac{1}{{\sqrt{5}}}}={\dfrac{{\sqrt{5}}}{5}} .\]所以二面角 $ F-BD-C $ 的余弦值为 $ {\dfrac{{\sqrt{5}}}{5}} $.
解法二:如图,取 $ BD $ 的中点 $ G $,连接 $ CG $,$ FG $. 由于 $ CB=CD $,因此 $ CG\perp BD $.
由于 $ CB=CD $,因此 $ CG\perp BD $.
又 $ FC\perp 平面 ABCD $,$ BD\subset 平面 ABCD $,
所以 $ FC\perp BD $.
由于 $ FC\cap CG=C $,$FC ,CG\subset 平面 FCG $,
所以 $ BD\perp 平面 FCG $,故 $ BD\perp FG $,
所以 $ \angle FGC $ 为二面角 $ F-BD-C $ 的平面角.
在等腰三角形 $ BCD $ 中,由于 $ \angle BCD=120^\circ $,因此 $ CG={\dfrac{1}{2}}CB $.
又 $ CB=CF $,所以 $ GF={\sqrt{CG^2+CF^2}}={\sqrt{5}}CG $,
故 $ \cos \angle FGC={\dfrac{{\sqrt{5}}}{5}} $,因此二面角 $ F-BD-C $ 的余弦值为 $ {\dfrac{{\sqrt{5}}}{5}} $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2