如图，几何体 $E - ABCD$ 是四棱锥，$\triangle ABD$ 为正三角形，$CB = CD,EC \perp BD$．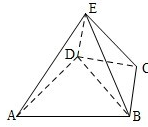
【难度】
【出处】
2012年高考山东卷（文）
【标注】
-
求证：$BE = DE$；标注答案略解析如图，设 $BD$ 中点为 $O$，连接 $OC,OE$，
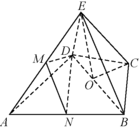则由 $BC = CD$ 知，$CO \perp BD$，
又已知 $CE \perp BD$，$ EC\cap CO=C $，
所以 $BD \perp $ 平面 $OCE$．
所以 $BD \perp OE$，
即 $OE$ 是 $BD$ 的垂直平分线，
所以 $BE = DE$． -
若 $\angle BCD = 120^\circ $，$M$ 为线段 $AE$ 的中点，求证：$DM\parallel $ 平面 $BEC$．标注答案略解析取 $AB$ 中点 $N$，连接 $MN,DM,DN$．$\because$ $M$ 是 $AE$ 的中点，
$\therefore$ $MN\parallel BE$，
$\because$ $\triangle ABD$ 是等边三角形，
$\therefore$ $DN \perp AB$．
由 $\angle BCD = 120^\circ $ 知，$\angle CBD = 30^\circ $，
所以 $\angle ABC = 60^\circ + 30^\circ = 90^\circ $，
即 $BC \perp AB$，
所以 $ND\parallel BC$，
所以平面 $MND\parallel $ 平面 $BEC$，
故 $DM\parallel $ 平面 $BEC$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
