如图,椭圆 $M:\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\left(a > b > 0\right)$ 的离心率为 $\dfrac{\sqrt 3 }{2}$,直线 $x = \pm a$ 和 $y = \pm b$ 所围成的矩形 $ABCD$ 的面积为 $ 8 $.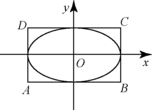

【难度】
【出处】
2012年高考山东卷(文)
【标注】
-
求椭圆 $M$ 的标准方程;标注答案略解析\[e = \dfrac{c}{a} = \dfrac{\sqrt 3 }{2} \Rightarrow \dfrac{{{a^2} - {b^2}}}{a^2} = \dfrac{3}{4}.\quad\cdots\cdots ① \]矩形 $ABCD$ 面积为 $ 8 $,即\[2a \cdot 2b = 8.\quad\cdots\cdots ② \]由 $ ①② $ 解得:\[a = 2,b = 1,\]所以椭圆 $M$ 的标准方程是\[\dfrac{x^2}{4} + {y^2} = 1.\]
-
设直线 $l:y = x + m\left(m \in {\mathbb{R}}\right)$ 与椭圆 $M$ 有两个不同的交点 $P,Q,l$ 与矩形 $ABCD$ 有两个不同的交点 $S , T$.求 $\dfrac{|PQ|}{|ST|}$ 的最大值及取得最大值时 $m$ 的值.标注答案略解析由已知得\[ {\begin{cases}
{x^2} + 4{y^2} = 4 \\
y = x + m \\
\end{cases}} \Rightarrow 5{x^2} + 8mx + 4{m^2} - 4 = 0 ,\]设 $P\left({x_1},{y_1}\right),Q\left({x_2},{y_2}\right)$,则\[\begin{split}{x_1} + {x_2} &= - \dfrac{8}{5}m,\\ {x_1}{x_2} &= \dfrac{{4{m^2} - 4}}{5},\end{split}\]由 $\Delta = 64{m^2} - 20\left(4{m^2} - 4\right) > 0$,得 $ - \sqrt 5 < m < \sqrt 5 $.\[\begin{split} |PQ| &= \sqrt 2 \sqrt {{{\left( { - \dfrac{8}{5}m} \right)}^2} - 4\cdot \dfrac{{4{m^2} - 4}}{5}} \\&= \dfrac{4\sqrt 2 }{5}\sqrt {5 - {m^2}} .\end{split}\]当 $l$ 过 $A$ 点时,$m = 1$,当 $l$ 过 $C$ 点时,$m = - 1$.
(i)当 $ - \sqrt 5 < m < - 1$ 时,有 $S\left( - m - 1, - 1\right),T\left(2,2 + m\right)$,所以\[ |ST| = \sqrt 2 \left(3 + m\right), \]因此\[\begin{split} \dfrac{|PQ|}{|ST|} &= \dfrac{4}{5}\sqrt {\dfrac{{5 - {m^2}}}{{{{\left(3 + m\right)}^2}}}} \\&= \dfrac{4}{5}\sqrt { - \dfrac{4}{t^2} + \dfrac{6}{t} - 1}, \end{split}\]其中 $t = m + 3$,由此知当 $\dfrac{1}{t} = \dfrac{3}{4}$,即\[t = \dfrac{4}{3},m = - \dfrac{5}{3} \in \left( - \sqrt 5 , - 1\right)\]时,$\dfrac{|PQ|}{|ST|}$ 取得最大值 $\dfrac{2\sqrt 5}{5} $.
(ii)由对称性,可知若 $1 < m < \sqrt 5 $,则当 $m = \dfrac{5}{3}$ 时,$\dfrac{|PQ|}{|ST|}$ 取得最大值 $\dfrac{2\sqrt 5}{5} $.
(iii)当 $ - 1 \leqslant m \leqslant 1$ 时,$|ST| = 2\sqrt 2 $,所以\[ \dfrac{|PQ|}{|ST|} = \dfrac{2}{5}\sqrt {5 - {m^2}} ,\]由此知,当 $m = 0$ 时,$\dfrac{|PQ|}{|ST|}$ 取得最大值 $\dfrac{2\sqrt 5}{5} $.
综上可知,当 $m = \pm \dfrac{5}{3}$ 和 $ 0 $ 时,$\dfrac{|PQ|}{|ST|}$ 取得最大值 $\dfrac{2\sqrt 5}{5} $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2