如图，证明命题" $ a $ 是平面 $ {\mathrm \pi } $ 内的一条直线，$ b $ 是 $ {\mathrm \pi } $ 外的一条直线（$ b $ 不垂直于 $ {\mathrm \pi }$），$ c $ 是直线 $ b $ 在 $ {\mathrm \pi } $ 上的投影，若 $ a\perp b $，则 $ a\perp c $ "为真；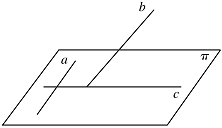
【难度】
【出处】
2012年高考陕西卷（理）
【标注】
【答案】
略
【解析】
证法一：如图，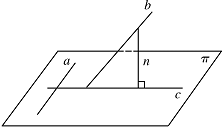
过直线 $ b $ 上任一点作平面 $ {\mathrm \pi } $ 的垂线 $ n $，
设直线 $ a$，$b$，$c$，$n $ 的方向向量分别是 $\overrightarrow a$，$\overrightarrow b$，$\overrightarrow c$，$\overrightarrow n $，则 $\overrightarrow b$，$\overrightarrow c$，$\overrightarrow n $ 共面．
根据平面向量基本定理，存在实数 $ \lambda$，$\mu $ 使得 $\overrightarrow c=\lambda \overrightarrow b+\mu \overrightarrow n $，则\[\begin{split} \overrightarrow a\cdot \overrightarrow c&=\overrightarrow a\cdot \left(\lambda \overrightarrow b+\mu \overrightarrow n\right)\\&=\lambda \left(\overrightarrow a\cdot \overrightarrow b\right)+\mu \left(\overrightarrow a\cdot \overrightarrow n\right),\end{split} \]因为 $ a\perp b $，所以 $\overrightarrow a\cdot \overrightarrow b=0 $，又因为 $ a\subset\mathrm \pi$，$n\perp{\mathrm \pi }$，
所以 $\overrightarrow a\cdot \overrightarrow n=0 $，故 $ \overrightarrow a\cdot \overrightarrow c=0 $，从而 $ a\perp c $．
证法二：如图，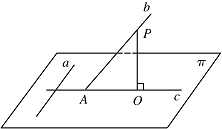
记 $ c\cap b=A $，$ P $ 为直线 $ b $ 上异于点 $ A $ 的任意一点，
过 $ P $ 作 $ PO\perp \mathrm \pi $，垂足为 $ O $，则 $ O\in c $．
$ \because PO \perp \mathrm \pi $，$a\subset \mathrm \pi $，$\therefore$ 直线 $ PO\perp a $，
又 $ a\perp b $，$ b \subset 平面 PAO $，$ PO\cap b=P $，
$ \therefore a\perp 平面 PAO $，又 $ c \subset 平面 PAO $，$ \therefore a\perp c $．
过直线 $ b $ 上任一点作平面 $ {\mathrm \pi } $ 的垂线 $ n $，设直线 $ a$，$b$，$c$，$n $ 的方向向量分别是 $\overrightarrow a$，$\overrightarrow b$，$\overrightarrow c$，$\overrightarrow n $，则 $\overrightarrow b$，$\overrightarrow c$，$\overrightarrow n $ 共面．
根据平面向量基本定理，存在实数 $ \lambda$，$\mu $ 使得 $\overrightarrow c=\lambda \overrightarrow b+\mu \overrightarrow n $，则\[\begin{split} \overrightarrow a\cdot \overrightarrow c&=\overrightarrow a\cdot \left(\lambda \overrightarrow b+\mu \overrightarrow n\right)\\&=\lambda \left(\overrightarrow a\cdot \overrightarrow b\right)+\mu \left(\overrightarrow a\cdot \overrightarrow n\right),\end{split} \]因为 $ a\perp b $，所以 $\overrightarrow a\cdot \overrightarrow b=0 $，又因为 $ a\subset\mathrm \pi$，$n\perp{\mathrm \pi }$，
所以 $\overrightarrow a\cdot \overrightarrow n=0 $，故 $ \overrightarrow a\cdot \overrightarrow c=0 $，从而 $ a\perp c $．
证法二：如图，
记 $ c\cap b=A $，$ P $ 为直线 $ b $ 上异于点 $ A $ 的任意一点，过 $ P $ 作 $ PO\perp \mathrm \pi $，垂足为 $ O $，则 $ O\in c $．
$ \because PO \perp \mathrm \pi $，$a\subset \mathrm \pi $，$\therefore$ 直线 $ PO\perp a $，
又 $ a\perp b $，$ b \subset 平面 PAO $，$ PO\cap b=P $，
$ \therefore a\perp 平面 PAO $，又 $ c \subset 平面 PAO $，$ \therefore a\perp c $．
答案
解析
备注
