略

当 $b = 1$，$c = - 1$，$n \geqslant 2$ 时，$f\left( x \right) = {x^n} + x - 1$．
$\because$ $f\left( {\dfrac{1}{2}} \right)f\left( 1 \right) = \left( {\dfrac{1}{2^n} - \dfrac{1}{2}} \right) \times 1 < 0$，
$\therefore f\left( x \right)$ 在 $\left( {\dfrac{1}{2},1} \right)$ 内存在零点．
又当 $x \in \left( {\dfrac{1}{2},1} \right)$ 时，$f'\left( x \right) = n{x^{n - 1}} + 1 > 0$，
$\therefore f\left( x \right)$ 在 $\left( {\dfrac{1}{2},1} \right)$ 上是单调递增的，
$\therefore f\left( x \right)$ 在 $\left( {\dfrac{1}{2},1} \right)$ 内存在唯一零点．

略

解法一：由题意知\[ \begin{cases}
- 1 \leqslant f\left( { - 1} \right) \leqslant 1, \\
- 1 \leqslant f\left( 1 \right) \leqslant 1, \\
\end{cases} \]即\[ \begin{cases}0 \leqslant b - c \leqslant 2, \\
- 2 \leqslant b + c \leqslant 0. \\
\end{cases} \]由图象知，$b+3c $ 在点 $\left(0,-2\right)$ 取到最小值 $-6$，在点 $\left(0,0\right)$ 取到最大值 $0$，
$\therefore$ $b+3c $ 的最小值为 $-6$，最大值为 $0$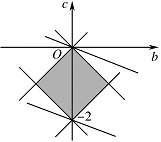． 解法二：由题意知\[ - 1 \leqslant f\left( { 1} \right)=1+ b+c \leqslant 1,即- 2 \leqslant b+c \leqslant 0. \quad \cdots \cdots ① \\ - 1 \leqslant f\left( { - 1} \right) = 1 - b + c \leqslant 1,即 - 2 \leqslant - b + c \leqslant 0. \quad \cdots \cdots ② \]$ ① \times2+ ② $ 得\[ - 6 \leqslant 2\left( {b + c} \right) + \left( { - b + c} \right) = b + 3c \leqslant 0,\]当 $b = 0$，$c = - 2$ 时，\[b + 3c = - 6;\]当 $b = c = 0$ 时，\[b + 3c = 0.\]所以 $b + 3c$ 的最小值为 $ - 6$，最大值为 $ 0$．
解法三：由题意知\[ \begin{cases}
f\left( { - 1} \right) = 1 - b + c, \\
f\left( 1 \right) = 1 + b + c. \\
\end{cases} \]解得\[\begin{split}b &= \dfrac{{f\left( 1 \right) - f\left( { - 1} \right)}}{2} , \\ c &= \dfrac{{f\left( 1 \right) + f\left( { - 1} \right) - 2}}{2}.\end{split}\]故\[b + 3c = 2f\left( 1 \right) + f\left( { - 1} \right) - 3.\]又 $\because - 1 \leqslant f\left( { - 1} \right) \leqslant 1$，$ - 1 \leqslant f\left( 1 \right) \leqslant 1$．
因此\[ - 6 \leqslant b + 3c \leqslant 0,\]当 $b = 0$，$c = - 2$ 时，$b + 3c = - 6$；
当 $b = c = 0$ 时，$b + 3c = 0$，
所以 $b + 3c$ 的最小值为 $ - 6$，最大值为 $ 0 $．

略

当 $n = 2$ 时，\[f\left( x \right) = {x^2} + bx + c.\]对任意 ${x_1},{x_2} \in \left[ { - 1,1} \right]$ 都有 $\left| {f\left( {x_1} \right) - f\left( {x_2} \right)} \right| \leqslant 4$ 等价于 $f\left( x \right)$ 在 $\left[ { - 1,1} \right]$ 上的最大值与最小值之差 $M \leqslant 4$，据此分类讨论如下：
① 当 $\left| {\dfrac{b}{2}} \right| > 1$，即 $\left| b \right| > 2$ 时，\[M = \left| {f\left( 1 \right) - f\left( { - 1} \right)} \right| = 2\left| b \right| > 4,\]与题设矛盾．
② 当 $ - 1 \leqslant - \dfrac{b}{2} < 0$，即 $0 < b \leqslant 2$ 时，\[M = f\left( 1 \right) - f\left( { - \dfrac{b}{2}} \right) = {\left( {\dfrac{b}{2} + 1} \right)^2} \leqslant 4\]恒成立．
③ 当 $0 \leqslant - \dfrac{b}{2} \leqslant 1$，即 $ - 2 \leqslant b \leqslant 0$ 时，\[M = f\left( { - 1} \right) - f\left( { - \dfrac{b}{2}} \right) = {\left( {\dfrac{b}{2} - 1} \right)^2} \leqslant 4\]恒成立．
综上可知，$ - 2 \leqslant b \leqslant 2$．