已知四棱锥 $P-ABCD$ 的底面是正方形，$PD=AD=4$，$PD$ 与底面成 $60^\circ$ 角，点 $H$ 在 $AD$ 上，且 $PH\perp ABCD$，点 $M$ 是 $PC$ 的中点．求：
【难度】
【出处】
2013年第二十四届“希望杯”全国数学邀请赛高二（二试）
【标注】
-
$DM$ 与 $BC$ 所成角的余弦值；标注答案$\dfrac{\sqrt2}{4}$解析取 $BC$ 中点记为 $E$，以 $HA,HE,HP$ 分别为 $x,y,z$ 轴建立空间直角坐标系，如图．
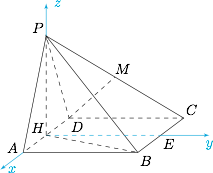根据题意，则有$$D(-2,0,0),M\left(-1,-2,\sqrt3\right),B(2,4,0),C(-2,4,0),$$因此，$$\overrightarrow{DM}=\left(1,-2,\sqrt3\right),\overrightarrow{BC}=(-4,0,0),$$设 $DM$ 与 $BC$ 所成角为 $\theta$，则$$\cos\theta=\left|\cos\left\langle\overrightarrow{DM},\overrightarrow{BC}\right\rangle\right|=\dfrac{\sqrt2}{4}.$$所以 $DM$ 与 $BC$ 所成角的余弦值为 $\dfrac{\sqrt2}{4}$． -
直线 $PC$ 与 $HB$ 间的距离．标注答案$\dfrac{8\sqrt{93}}{31}$解析由题可知$$\overrightarrow{PC}=\left(-2,4,-2\sqrt3\right),\overrightarrow{HB}=(2,4,0),$$设点 $F$ 在直线 $HB$ 上，点 $G$ 在直线 $PC$ 上，则有$$\overrightarrow{HG}=\mu\overrightarrow{HB},\overrightarrow{PG}=\lambda\overrightarrow{PC},$$因此，计算得$$F\left(2\mu,4\mu,0\right),G\left(-2\lambda,4\lambda,-2\sqrt3\lambda+2\sqrt3\right),$$设线段 $FG$ 是直线 $HB,PC$ 的公垂线，则有$$\begin{cases}\overrightarrow{FG}\cdot\overrightarrow{HB}=0,\\\overrightarrow{FG}\cdot\overrightarrow{PC}=0\end{cases}$$整理得$$\begin{cases}5\mu=3\lambda,\\3\mu-8\lambda+3=0,\end{cases}$$解得 $\lambda=\dfrac{15}{31},\mu=\dfrac{9}{31}$，因此$$F\left(\dfrac{18}{31},\dfrac{36}{31},0\right),G\left(-\dfrac{30}{31},\dfrac{60}{31},\dfrac{32\sqrt3}{31}\right),$$所以 $|EF|=\dfrac{8\sqrt{93}}{31}$，故直线 $PC$ 与 $HB$ 之间的距离为 $\dfrac{8\sqrt{93}}{31}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
