椭圆 $C:x^2+\dfrac{y^2}{4}=1$,在第一象限内的一段弧即为 $AB$,点 $P(x,y)$ 在弧 $AB$ 上,如图.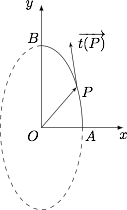

【难度】
【出处】
2012年第二十三届“希望杯”全国数学邀请赛高二(二试)
【标注】
-
用 $\overrightarrow{t(P)}$ 表示椭圆 $C$ 在点 $P$ 处的切线的单位向量,方向是依椭圆的逆时针走向,求向量 $\overrightarrow{t}(P)$ 的解析式;标注答案$\overrightarrow{t(P)}=\left(-\dfrac{\sqrt{1-x^2}}{\sqrt{1+3x^2}},\dfrac{2x}{\sqrt{1+3x^2}}\right)$解析根据圆锥曲线上一点的切线方程,可得切线斜率为 $-\dfrac{4x}{y}$,因此点 $P$ 处切线的方向向量为$$\left(1,-\dfrac{4x}{y}\right),$$根据点 $P$ 在椭圆上,结合单位化,得$$\overrightarrow{t(P)}=\left(-\dfrac{\sqrt{1-x^2}}{\sqrt{1+3x^2}},\dfrac{2x}{\sqrt{1+3x^2}}\right).$$
-
令函数 $f(P)=\overrightarrow{t(P)}\cdot\overrightarrow{OP}$,写出函数 $f(P)\equiv f(x)$ 的解析式;标注答案$f(P)\equiv f(x)=\dfrac{3x\sqrt{1-x^2}}{\sqrt{1+3x^2}}$($0\leqslant x\leqslant 1$)解析因为 $\overrightarrow{OP}=\left(x,2\sqrt{1-x^2}\right)$,所以$$f(P)=\overrightarrow{t(P)}\cdot\overrightarrow{OP}=\dfrac{3x\sqrt{1-x^2}}{\sqrt{1+3x^2}},$$因此 $f(P)\equiv f(x)=\dfrac{3x\sqrt{1-x^2}}{\sqrt{1+3x^2}}$($0\leqslant x\leqslant 1$).
-
求函数 $f(P)$ 的最大值及取最大值时的点 $P$ 的坐标,并确定函数 $f(P)\equiv f(x)$ 的值域.标注答案$1$,$\left(\dfrac{\sqrt3}{3},\dfrac{2\sqrt6}{3}\right)$;$[0,1]$解析令 $m=\dfrac{x^2\left(1-x^2\right)}{1+3x^2}$,其中 $0\leqslant x\leqslant1$,则$$0\leqslant m<1,$$因此有$$(1+3x^2)m=x^2(1-x^2),$$令 $t=x^2$,则 $t\in[0,1]$,题意即$$x^2+(3m-1)t+m=0,$$在 $[0,1]$ 上有解,因此$$\Delta=9m^2-10m+1\geqslant0,$$解得 $0\leqslant m\leqslant\dfrac19$,此时对应方程的解均为正数,符合题意;
因此,函数 $f(P)\equiv f(x)$ 的值域是 $[0,1]$,且当 $P\left(\dfrac{\sqrt3}{3},\dfrac{2\sqrt6}{3}\right)$ 时,函数取得最大值为 $1$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3