已知正三棱锥底面的一个顶点与它所在的侧面的重心的距离为 $4$，求此正三棱锥的体积的最大值．
【难度】
【出处】
2012年第二十三届“希望杯”全国数学邀请赛高二（二试）
【标注】
【答案】
$18$
【解析】
如图，设 $D$ 为侧面 $PBC$ 的重心，$O$ 为底面 $ABC$ 的中心．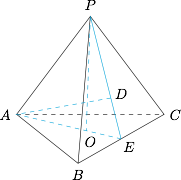
由正四棱锥 $P-ABC$，则 $PO\perp ABC$，设 $AB=a,PB=b$，则有$$AE=\dfrac{\sqrt3}{2}a,AD=4,DE=\dfrac13PE=\dfrac13\cdot\sqrt{b^2-\dfrac14a^2},$$此时有$$PO=\sqrt{PE^2-OE^2}=\sqrt{b^2-\dfrac13a^2},$$在 $\triangle ADE$ 和 $\triangle POE$ 中，有$$\cos\angle DEA=\dfrac{AE^2+DE^2-AD^2}{2\cdot AE\cdot DE}=\dfrac{OE}{PE},$$整理得$$5a^2+b^2=144,$$再结合 $b^2\geqslant\dfrac13a^2$，得 $a\leqslant3\sqrt3$，故体积为\[\begin{split}V&=\dfrac13\cdot S_{\triangle ABC}\cdot PO\\&=\dfrac{1}{3\sqrt2}\cdot\sqrt{(54-2a^2)\cdot a^2\cdot a^2}\\&\leqslant\dfrac{1}{3\sqrt2}\cdot\sqrt{\left(\dfrac{54-2a^2+a^2+a^2}{3}\right)^3}\\&=18.\end{split}\]当且仅当 $a=3\sqrt2$ 时，等号成立，因此此正三棱锥的体积的最大值为 $18$．
由正四棱锥 $P-ABC$，则 $PO\perp ABC$，设 $AB=a,PB=b$，则有$$AE=\dfrac{\sqrt3}{2}a,AD=4,DE=\dfrac13PE=\dfrac13\cdot\sqrt{b^2-\dfrac14a^2},$$此时有$$PO=\sqrt{PE^2-OE^2}=\sqrt{b^2-\dfrac13a^2},$$在 $\triangle ADE$ 和 $\triangle POE$ 中，有$$\cos\angle DEA=\dfrac{AE^2+DE^2-AD^2}{2\cdot AE\cdot DE}=\dfrac{OE}{PE},$$整理得$$5a^2+b^2=144,$$再结合 $b^2\geqslant\dfrac13a^2$，得 $a\leqslant3\sqrt3$，故体积为\[\begin{split}V&=\dfrac13\cdot S_{\triangle ABC}\cdot PO\\&=\dfrac{1}{3\sqrt2}\cdot\sqrt{(54-2a^2)\cdot a^2\cdot a^2}\\&\leqslant\dfrac{1}{3\sqrt2}\cdot\sqrt{\left(\dfrac{54-2a^2+a^2+a^2}{3}\right)^3}\\&=18.\end{split}\]当且仅当 $a=3\sqrt2$ 时，等号成立，因此此正三棱锥的体积的最大值为 $18$．
答案
解析
备注
