如图，在四棱锥 $ P-ABCD $ 中，底面 $ ABCD $ 是矩形，$ PA\perp 底面 ABCD $，$ E $ 是 $ PC $ 的中点．已知 $ AB=2$，$AD=2{\sqrt{2}}$，$PA=2 $．求：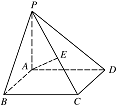
【难度】
【出处】
2012年高考上海卷（理）
【标注】
-
三角形 $ PCD $ 的面积；标注答案略解析因为 $ PA\perp 底面 ABCD $，所以 $ PA\perp CD $．
又 $ AD\perp CD $，所以 $ CD\perp 平面 PAD $，从而 $ CD\perp PD $．
因为 $ PD=\sqrt{2^2+\left(2 \sqrt 2\right)^2 }=2{\sqrt{3}}$，$CD=2 $，
所以三角形 $ PCD $ 的面积为\[ {\dfrac{1}{2}}\times 2\times 2{\sqrt{3}}=2{\sqrt{3}} .\] -
异面直线 $ BC $ 与 $ AE $ 所成的角的大小．标注答案略解析解法一：如图所示，建立空间直角坐标系，
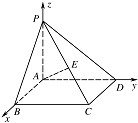则 $ B\left(2,0,0\right)$，$C\left(2,2{\sqrt{2}},0\right)$，$E\left(1, {\sqrt{2}},1\right) $，$ {\overrightarrow {AE}}=\left(1,{\sqrt{2}},1\right)$，${\overrightarrow {BC}}=\left(0,2{\sqrt{2}},0\right) $．
设 $ {\overrightarrow {AE}} $ 与 $ {\overrightarrow {BC}} $ 的夹角为 $ \theta $，则\[ \begin{split}\cos \theta &= \dfrac{{\overrightarrow {AE}}\cdot {\overrightarrow {BC}} }{ \left|{\overrightarrow {AE}} \right| \left|{\overrightarrow {BC}} \right|} \\&={\dfrac{4}{2\times 2{\sqrt{2}}}}={\dfrac{{\sqrt{2}}}{2}},\end{split}\]所以\[\theta ={\dfrac{{\mathrm \pi } }{4}}, \]由此知，异面直线 $ BC $ 与 $ AE $ 所成的角的大小是 $ {\dfrac{{\mathrm \pi } }{4}} $．
解法二：如图所示，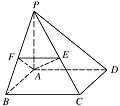
取 $ PB $ 的中点 $ F $，连接 $ EF$，$AF $，则 $ EF\parallel BC $，
从而 $ \angle AEF $（或其补角）是异面直线 $ BC $ 与 $ AE $ 所成的角．
在 $ \triangle AEF $ 中，由 $ EF={\sqrt{2}}$，$AF={\sqrt{2}} $，$ AE=2 $，
知 $ \triangle AEF $ 是等腰直角三角形，所以 $ \angle AEF={\dfrac{{\mathrm \pi } }{4}} $，
因此，异面直线 $ BC $ 与 $ AE $ 所成的角的大小是 $ {\dfrac{{\mathrm \pi } }{4}} $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
