如图，在三棱锥 $ P-ABC $ 中，$ PA\perp 底面 ABC $，$ D $ 是 $ PC $ 的中点．已知 $ \angle BAC={\dfrac{{\mathrm \pi } }{2}} $，$ AB=2$，$AC=2{\sqrt{3}}$，$PA=2 $．求：
【难度】
【出处】
2012年高考上海卷（文）
【标注】
-
三棱锥 $ P-ABC $ 的体积；标注答案略解析\[ \begin{split}S_{\triangle ABC}&=\dfrac 1 2 AB\cdot AC={\dfrac{1}{2}}\times 2\times 2{\sqrt{3}}=2{\sqrt{3}},\end{split}\]三棱锥 $ P-ABC $ 的体积为\[ \begin{split}V={\dfrac{1}{3}}S_{\triangle ABC}\times PA={\dfrac{1}{3}}\times 2{\sqrt{3}}\times 2={\dfrac{4}{3}}{\sqrt{3}}. \end{split}\]
-
异面直线 $ BC $ 与 $ AD $ 所成的角的大小（结果用反三角函数值表示）．标注答案略解析如图，
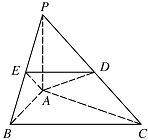取 $ PB $ 的中点 $ E $，连接 $ DE$，$AE $，则 $ ED\parallel BC $，
所以 $ \angle ADE $（或其补角）是异面直线 $ BC $ 与 $ AD $ 所成的角．
在 $ \triangle ADE $ 中，$DE=2$，$AE={\sqrt{2}}$，$AD=2 $，所以\[ \cos \angle ADE={\dfrac{2^2+2^2-2}{2\times 2\times 2}}={\dfrac{3}{4}} ,\]所以\[ \angle ADE=\arccos {\dfrac{3}{4}}. \]因此，异面直线 $ BC $ 与 $ AD $ 所成的角的大小是 $ \arccos {\dfrac{3}{4}} $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
