如图，过椭圆外一点引椭圆的两条切线 $PA$ 与 $PB$．椭圆上一点 $C$ 处的切线与 $PA,PB$ 分别交于 $M,N$，即椭圆与 $\triangle PMN$ 旁切．求证：$MN$ 对椭圆的焦点 $F$ 的张角大小与 $C$ 点的位置无关．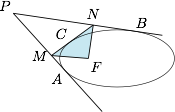
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
设椭圆的另一个焦点为 $E$，以 $F$ 为圆心，长轴长为半径作圆，则 $E$ 点关于 $PA,PB,MN$ 的对称点 $A_1,B_1,C_1$ 均在圆上，如图．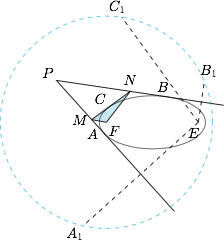
接下来想办法将 $\angle MFN$ 从难处理的椭圆中转移到容易处理的圆中．如图，过 $A_1,B_1,C_1$ 分别作直线 $P'A_1,P'B_1,M'N'$ 与直线 $PA,PB,MN$ 平行，这相当于以 $E$ 为中心，将 $PMA,PNB$ 放大到原来的两倍．因此类似的将 $F$ 放大到 $F'$ 的位置，其中 $F'E=2FE$．这样就有 $\angle MFN=\angle M'F'N'$．
最后我们集中精力在圆中解决这个问题（如下图）．
设 $P'A_1,P'B_1,M'N'$ 分别与圆交于点 $X,Y,Z$，连接 $F'X,F'Y,F'Z,ZX,ZY$．
由于 $F$ 平分 $F'E$ 且为圆心，于是 $F'X\perp P'A_1,F'Y\perp P'B_1,F'Z\perp M'N'$，进而 $Z,M',X,F'$ 四点共圆，$Z,Y,N',F'$ 四点共圆．
于是所求角$$\begin{split} \angle M'F'N'=&\angle M'F'Z+\angle N'F'Z\\=&\angle M'XZ+\left(\pi-\angle ZYB_1\right)\\=&\pi-\angle A_1XZ+\pi-\angle ZYB_1.\end{split} $$因此 $M'F'N'$ 的大小始终为弧 $A_1C_1B_1$ 所对的圆周角，与 $C_1$ 的位置无关．进而 $MFN$ 的大小是固定的，而与 $C$ 的位置无关，原命题得证．
最后给出所有辅助线的“全家福”．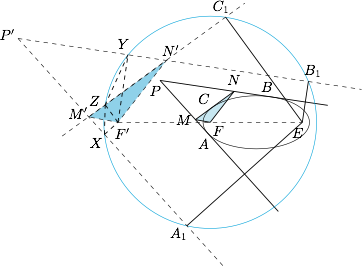
接下来想办法将 $\angle MFN$ 从难处理的椭圆中转移到容易处理的圆中．如图，过 $A_1,B_1,C_1$ 分别作直线 $P'A_1,P'B_1,M'N'$ 与直线 $PA,PB,MN$ 平行，这相当于以 $E$ 为中心，将 $PMA,PNB$ 放大到原来的两倍．因此类似的将 $F$ 放大到 $F'$ 的位置，其中 $F'E=2FE$．这样就有 $\angle MFN=\angle M'F'N'$．最后我们集中精力在圆中解决这个问题（如下图）．设 $P'A_1,P'B_1,M'N'$ 分别与圆交于点 $X,Y,Z$，连接 $F'X,F'Y,F'Z,ZX,ZY$．由于 $F$ 平分 $F'E$ 且为圆心，于是 $F'X\perp P'A_1,F'Y\perp P'B_1,F'Z\perp M'N'$，进而 $Z,M',X,F'$ 四点共圆，$Z,Y,N',F'$ 四点共圆．
于是所求角$$\begin{split} \angle M'F'N'=&\angle M'F'Z+\angle N'F'Z\\=&\angle M'XZ+\left(\pi-\angle ZYB_1\right)\\=&\pi-\angle A_1XZ+\pi-\angle ZYB_1.\end{split} $$因此 $M'F'N'$ 的大小始终为弧 $A_1C_1B_1$ 所对的圆周角，与 $C_1$ 的位置无关．进而 $MFN$ 的大小是固定的，而与 $C$ 的位置无关，原命题得证．
最后给出所有辅助线的“全家福”．
答案
解析
备注
