题目

查看数据源：599165b52bfec200011dddb2

函数 $f\left(x\right) = 6{\cos ^2}\dfrac{\omega x}{2} + \sqrt 3 \sin \omega x - 3\left( {\omega > 0} \right)$ 在一个周期内的图象如图所示，$A$ 为图象的最高点，$B,C$ 为图象与 $x$ 轴的交点，且 $\triangle ABC$ 为正三角形．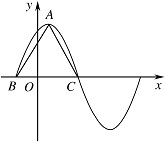

【难度】

【出处】

2012年高考四川卷（理）

【标注】

求 $\omega $ 的值及函数 $f\left(x\right)$ 的值域；
标注
答案

略

解析

由已知可得，\[\begin{split}f\left( x \right) & = 3\cos \omega x + \sqrt 3 \sin \omega x \\& = 2\sqrt 3 \sin \left( {\omega x + \dfrac{\mathrm \pi }{3}} \right).\end{split}\]又正三角形 $ABC$ 的高为 $2\sqrt 3 $，从而 $BC = 4$．
所以函数 $f\left( x \right)$ 的周期 $T = 4 \times 2 = 8$，即\[\dfrac{{2{\mathrm \pi }}}{\omega } = 8,\omega = \dfrac{\mathrm \pi }{4}.\]函数 $f\left( x \right)$ 的值域为 $\left[ { - 2\sqrt 3 ,2\sqrt 3 } \right]$．
若 $f\left({x_0}\right) = \dfrac{8\sqrt 3 }{5}$，且 ${x_0} \in \left( { - \dfrac{10}{3},\dfrac{2}{3}} \right)$，求 $f\left({x_0} + 1\right)$ 的值．
标注
答案

略

解析

因为 $f\left( {x_0} \right) = \dfrac{8\sqrt 3 }{5}$，由（1）有\[f\left( {x_0} \right) = 2\sqrt 3 \sin \left( {\dfrac{{{\mathrm \pi }{x_0}}}{4} + \dfrac{\mathrm \pi }{3}} \right) = \dfrac{8\sqrt 3 }{5},\]即 $\sin \left( {\dfrac{{{\mathrm \pi }{x_0}}}{4} + \dfrac{\mathrm \pi }{3}} \right) = \dfrac{4}{5}$．由 ${x_0} \in \left( { - \dfrac{10}{3},\dfrac{2}{3}} \right)$，知\[\dfrac{{{\mathrm \pi }{x_0}}}{4} + \dfrac{\mathrm \pi }{3} \in \left( { - \dfrac{\mathrm \pi }{2},\dfrac{\mathrm \pi }{2}} \right).\]所以\[\cos \left( {\dfrac{{{\mathrm \pi }{x_0}}}{4} + \dfrac{\mathrm \pi }{3}} \right) = \sqrt {1 - {{\left( {\dfrac{4}{5}} \right)}^2}} = \dfrac{3}{5}.\]故\[\begin{split}f\left( {{x_0} + 1} \right) &= 2\sqrt 3 \sin \left( {\dfrac{{{\mathrm \pi }{x_0}}}{4} + \dfrac{\mathrm \pi }{4} + \dfrac{\mathrm \pi }{3}} \right)\\& = 2\sqrt 3 \sin \left[ {\left( {\dfrac{{{\mathrm \pi }{x_0}}}{4} + \dfrac{\mathrm \pi }{3}} \right) + \dfrac{\mathrm \pi }{4}} \right]\\&= 2\sqrt 3 \left[ {\sin \left( {\dfrac{{{\mathrm \pi }{x_0}}}{4} + \dfrac{\mathrm \pi }{3}} \right)\cos \dfrac{\mathrm \pi }{4} + \cos \left( {\dfrac{{{\mathrm \pi }{x_0}}}{4} + \dfrac{\mathrm \pi }{3}} \right)\sin \dfrac{\mathrm \pi }{4}} \right]\\&= 2\sqrt 3 \left( {\dfrac{4}{5} \times \dfrac{\sqrt 2 }{2} + \dfrac{3}{5} \times \dfrac{\sqrt 2 }{2}} \right) \\&= \dfrac{7\sqrt 6 }{5}.\end{split}\]

题目问题1 答案1 解析1 备注1 问题2 答案2 解析2

因为 $f\left( {x_0} \right) = \dfrac{8\sqrt 3 }{5}$，由（1）有\[f\left( {x_0} \right) = 2\sqrt 3 \sin \left( {\dfrac{{{\mathrm \pi }{x_0}}}{4} + \dfrac{\mathrm \pi }{3}} \right) = \dfrac{8\sqrt 3 }{5},\]即 $\sin \left( {\dfrac{{{\mathrm \pi }{x_0}}}{4} + \dfrac{\mathrm \pi }{3}} \right) = \dfrac{4}{5}$．由 ${x_0} \in \left( { - \dfrac{10}{3},\dfrac{2}{3}} \right)$，知\[\dfrac{{{\mathrm \pi }{x_0}}}{4} + \dfrac{\mathrm \pi }{3} \in \left( { - \dfrac{\mathrm \pi }{2},\dfrac{\mathrm \pi }{2}} \right).\]所以\[\cos \left( {\dfrac{{{\mathrm \pi }{x_0}}}{4} + \dfrac{\mathrm \pi }{3}} \right) = \sqrt {1 - {{\left( {\dfrac{4}{5}} \right)}^2}} = \dfrac{3}{5}.\]故\[\begin{split}f\left( {{x_0} + 1} \right) &= 2\sqrt 3 \sin \left( {\dfrac{{{\mathrm \pi }{x_0}}}{4} + \dfrac{\mathrm \pi }{4} + \dfrac{\mathrm \pi }{3}} \right)\\& = 2\sqrt 3 \sin \left[ {\left( {\dfrac{{{\mathrm \pi }{x_0}}}{4} + \dfrac{\mathrm \pi }{3}} \right) + \dfrac{\mathrm \pi }{4}} \right]\\&= 2\sqrt 3 \left[ {\sin \left( {\dfrac{{{\mathrm \pi }{x_0}}}{4} + \dfrac{\mathrm \pi }{3}} \right)\cos \dfrac{\mathrm \pi }{4} + \cos \left( {\dfrac{{{\mathrm \pi }{x_0}}}{4} + \dfrac{\mathrm \pi }{3}} \right)\sin \dfrac{\mathrm \pi }{4}} \right]\\&= 2\sqrt 3 \left( {\dfrac{4}{5} \times \dfrac{\sqrt 2 }{2} + \dfrac{3}{5} \times \dfrac{\sqrt 2 }{2}} \right) \\&= \dfrac{7\sqrt 6 }{5}.\end{split}\]