如图,在三棱锥 $P - ABC$ 中,$\angle APB = {90^ \circ },\angle PAB = {60^ \circ }$,$AB = BC = CA$,平面 $PAB \perp $ 平面 $ABC$.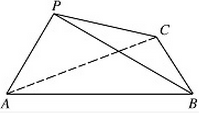

【难度】
【出处】
2012年高考四川卷(理)
【标注】
-
求直线 $PC$ 与平面 $ABC$ 所成角的正弦值;标注答案略解析解法一:如图:
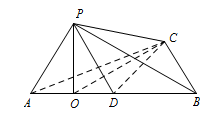 设 $ AB $ 的中点为 $ D $,$ AD $ 的中点为 $ O $,连接 $ PO$,$ PD $,$ CO $,$CD $.因为 $ AB=BC=CA $,所以 $ CD\perp AB $.
设 $ AB $ 的中点为 $ D $,$ AD $ 的中点为 $ O $,连接 $ PO$,$ PD $,$ CO $,$CD $.因为 $ AB=BC=CA $,所以 $ CD\perp AB $.
因为 $ \angle APB=90^\circ $,$\angle PAB=60^\circ $.
所以 $ \triangle PAD $ 为等边三角形,所以 $ PO\perp AD $.
又平面 $ PAB\perp $ 平面 $ ABC $,平面 $ PAB\cap $ 平面 $ ABC=AD $,
所以 $ PO\perp $ 平面 $ ABC $,所以 $ \angle OCP $ 为直线 $ PC $ 与平面 $ ABC $ 所成的角.
不妨设 $PA=2 $,则\[ OD =1, PO =\sqrt{3}, AB=4\]在 $ \mathrm{Rt}\triangle OCD $ 中,\[ CO =\sqrt{O{{D}^{2}}+C{{D}^{2}}} =\sqrt{13}, \]所以,在 $ \mathrm{Rt}\triangle POC $ 中,$ PC=4 $,\[\sin \angle OCP =\frac{PO}{PC} =\frac{\sqrt{3}}{4} .\]故直线 $ PC $ 与平面 $ ABC $ 所成的角的正弦值为 $\dfrac{\sqrt{3}}{4}$.
解法二:
设 $ AB $ 中点为 $ D $,作 $ PO\perp AB $ 于点 $ O $,连接 $ CD $.
因为平面 $ PAB\perp $ 平面 $ ABC $,平面 $ PAB\cap $ 平面 $ ABC=AD $,
所以 $PO \perp $ 平面 $ABC$.
所以 $PO \perp CD$.
由 $AB = BC = CA$,知 $CD \perp AB$.
设 $E$ 为 $AC$ 中点,则 $EO\parallel CD$,从而 $OE \perp PO$,$OE \perp AB$.
如图,以 $O$ 为坐标原点,$OB,OE,OP$ 所在直线分别为 $x,y,z$ 轴建立空间直角坐标系 $O - xyz$.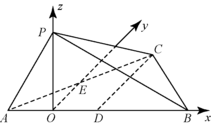 不妨设 $PA = 2$,由已知可得,\[AB = 4,OA = OD = 1,OP = \sqrt 3 ,CD = 2\sqrt 3 .\]所以 $O\left( {0,0,0} \right)$,$ A\left( { - 1,0,0} \right) $,$ C\left( {1,2\sqrt 3 ,0} \right) $,$P\left( {0,0,\sqrt 3 } \right)$,所以\[\overrightarrow {CP} = \left( { - 1, - 2\sqrt 3 ,\sqrt 3 } \right),\]而 $\overrightarrow {OP} = \left( {0,0,\sqrt 3 } \right)$ 为平面 $ABC$ 的一个法向量.
不妨设 $PA = 2$,由已知可得,\[AB = 4,OA = OD = 1,OP = \sqrt 3 ,CD = 2\sqrt 3 .\]所以 $O\left( {0,0,0} \right)$,$ A\left( { - 1,0,0} \right) $,$ C\left( {1,2\sqrt 3 ,0} \right) $,$P\left( {0,0,\sqrt 3 } \right)$,所以\[\overrightarrow {CP} = \left( { - 1, - 2\sqrt 3 ,\sqrt 3 } \right),\]而 $\overrightarrow {OP} = \left( {0,0,\sqrt 3 } \right)$ 为平面 $ABC$ 的一个法向量.
设 $\alpha $ 为直线 $PC$ 与平面 $ABC$ 所成的角,则\[\sin \alpha = \left| {\dfrac{{\overrightarrow {CP} \cdot \overrightarrow {OP} }}{{\left| {\overrightarrow {CP} } \right| \cdot \left| {\overrightarrow {OP} } \right|}}} \right| = \left| {\dfrac{0 + 0 + 3}{{\sqrt {16} \cdot \sqrt 3 }}} \right| = \dfrac{\sqrt 3 }{4}.\]故直线 $PC$ 与平面 $ABC$ 所成的角的正弦值为 $ \dfrac{\sqrt 3 }{4}$. -
求二面角 $B - AP - C$ 的余弦值.标注答案略解析解法一:
过 $ D $ 作 $ DE\perp AP $ 于 $ E $,连接 $ CE $.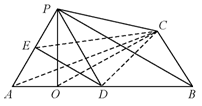 由已知可得,$ CD\perp $ 平面 $ PAB $.
由已知可得,$ CD\perp $ 平面 $ PAB $.
所以 $CD\perp PA$,所以 $PA\perp$ 平面 $CDE$,从而 $PA\perp CE $.
所以 $ \angle CED $ 为二面角 $ B-AP-C $ 的平面角.
由(1)知,$ DE=\sqrt{3} $.在 $ {\mathrm{Rt}}\triangle CDE $ 中,$ CE=\sqrt{15} $,\[ \cos \angle CED=\frac{DE}{EC}=\frac{\sqrt{5}}{5}.\]故二面角 $ B-AP-C $ 的余弦值为 $\dfrac{\sqrt 5 }{5} $.
解法二:
由(1)有,\[\overrightarrow {AP} = \left( {1,0,\sqrt 3 } \right), \overrightarrow {AC} = \left( {2,2\sqrt 3 ,0} \right).\] 设平面 $APC$ 的一个法向量为 $\overrightarrow n = \left( {{x_1},{y_1},{z_1}} \right)$,则\[\begin{cases} \overrightarrow n ⊥ \overrightarrow {AP} , \\
设平面 $APC$ 的一个法向量为 $\overrightarrow n = \left( {{x_1},{y_1},{z_1}} \right)$,则\[\begin{cases} \overrightarrow n ⊥ \overrightarrow {AP} , \\
\overrightarrow n ⊥ \overrightarrow {AC} . \\
\end{cases} \Rightarrow \begin{cases}\overrightarrow n \cdot \overrightarrow {AP} = 0, \\
\overrightarrow n \cdot \overrightarrow {AC} = 0. \\
\end{cases} \Rightarrow \begin{cases}\left( {{x_1},{y_1},{z_1}} \right) \cdot \left( {1,0,\sqrt 3 } \right) = 0, \\
\left( {{x_1},{y_1},{z_1}} \right) \cdot \left( {2,2\sqrt 3 ,0} \right) = 0. \\
\end{cases}\]从而\[\begin{cases}{x_1} + \sqrt 3 {z_1} = 0, \\
2{x_1} + 2\sqrt 3 {y_1} = 0. \\
\end{cases}\]取 ${x_1} = - \sqrt 3 $,则 ${y_1} = 1$,${z_1} = 1$,所以\[\overrightarrow n = \left( { - \sqrt 3 ,1,1} \right).\]设二面角 $B - AP - C$ 的平面角为 $\beta $,易知 $\beta $ 为锐角.
而平面 $ABP$ 的一个法向量为 $\overrightarrow m = \left( {0,1,0} \right)$,则\[\cos \beta = \left| {\dfrac{\overrightarrow n \cdot \overrightarrow m }{{\left| {\overrightarrow n}\right| \cdot \left| {\overrightarrow m } \right|} }} \right| = \left| {\dfrac{1}{\sqrt {3 + 1 + 1}}} \right| = \dfrac{\sqrt 5 }{5}.\]故二面角 $B - AP - C$ 的余弦值为 $ \dfrac{\sqrt 5 }{5}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2