如图,设椭圆的中心为原点 $O$,长轴在 $x$ 轴上,上顶点为 $A$,左右焦点分别为 ${F_1},{F_2}$,线段 $O{F_1},O{F_2}$ 的中点分别为 ${B_1},{B_2}$,且 $\triangle A{B_1}{B_2}$ 是面积为 $ 4 $ 的直角三角形.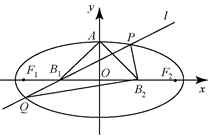

【难度】
【出处】
2012年高考重庆卷(理)
【标注】
-
求该椭圆的离心率和标准方程;标注答案略解析如图,设所求椭圆的标准方程为\[\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\left( {a > b > 0} \right),\]右焦点为 ${F_2}\left( {c,0} \right)$.因 $\triangle A{B_1}{B_2}$ 是直角三角形,又 $\left| {A{B_1}} \right| = \left| {A{B_2}} \right|$,
故 $\angle {B_1}A{B_2}$ 为直角,因此 $\left| {OA} \right| = \left| {O{B_2}} \right|$,得 $b = \dfrac{c}{2}$.
结合 ${c^2} = {a^2} - {b^2}$,得\[4{b^2} = {a^2} - {b^2},\]故\[{a^2} = 5{b^2},{c^2} = 4{b^2},\]所以离心率\[{e} = \dfrac{c}{a} = \dfrac{2}{5}\sqrt 5, \]在 $\operatorname{{\mathrm{Rt}}} \triangle A{B_1}{B_2}$ 中 $OA \perp {B_1}{B_2}$,故\[\begin{split}{S_{\triangle A{B_1}{B_2}}} &= \dfrac{1}{2} \cdot \left| {{B_1}{B_2}} \right| \cdot \left| {OA} \right| \\&= \left| {O{B_2}} \right| \cdot \left| {OA} \right| \\&= \dfrac{c}{2} \cdot b = {b^2} ,\end{split}\]由题设条件 ${S_{\triangle A{B_1}{B_2}}} = 4$,得 ${b^2} = 4$,从而\[{a^2} = 5{b^2} = 20,\]因此所求椭圆的标准方程为:$\dfrac{x^2}{20} + \dfrac{y^2}{4} = 1$. -
过 ${B_1}$ 作直线 $l$ 交椭圆于 $P,Q$ 两点,使 $P{B_2} \perp Q{B_2}$,求直线 $l$ 的方程.标注答案略解析由(1)知 ${B_1}\left( { - 2,0} \right),{B_2}\left( {2,0} \right),$ 由题意知直线 $l$ 的倾斜角不为 $ 0, $ 故可设直线 $l$ 的方程为\[x = my - 2,\]代入椭圆方程得\[\left( {{m^2} + 5} \right){y^2} - 4my - 16 = 0,\]设 $P\left( {{x_1},{y_1}} \right)$、$Q\left( {{x_2},{y_2}} \right)$,则 ${y_1},{y_2}$ 是上面方程的两根,因此\[\begin{split}{y_1} + {y_2} &= \dfrac{4m}{{{m^2} + 5}},\\ {y_1} \cdot {y_2} &= - \dfrac{16}{{{m^2} + 5}},\end{split}\]又\[\begin{split}\overrightarrow {{B_2}P} &= \left( {{x_1} - 2,{y_1}} \right),\\ \overrightarrow {{B_2}Q} &= \left( {{x_2} - 2,{y_2}} \right),\end{split}\]所以\[\begin{split}\overrightarrow {{B_2}P} \cdot \overrightarrow {{B_2}Q} &= \left( {{x_1} - 2} \right)\left( {{x_2} - 2} \right) + {y_1}{y_2}\\
&= \left( {m{y_1} - 4} \right)\left( {m{y_2} - 4} \right) + {y_1} {y_2}\\
&= \left( {{m^2} + 1} \right){y_1}{y_2} - 4m\left( {{y_1} + {y_2}} \right) + 16\\
&= - \dfrac{{16\left( {{m^2} + 1} \right)}}{{{m^2} + 5}} - \dfrac{{16{m^2}}}{{{m^2} + 5}} + 16\\
&= - \dfrac{{16{m^2} - 64}}{{{m^2} + 5}},\end{split}\]由 $P{B_2} \perp Q{B_2}$,得\[\overrightarrow {{B_2}P} \cdot \overrightarrow {{B_2}Q} = 0,\]即\[16{m^2} - 64 = 0,\]解得 $m = \pm 2$.
所以满足条件的直线有两条,其方程分别为\[x + 2y + 2 = 0 和 x - 2y + 2 = 0.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2