如图,在直三棱柱 $ ABC-A_1B_1C_1 $ 中,$ AB=4$,$AC=BC=3 $,$ D $ 为 $ AB $ 的中点.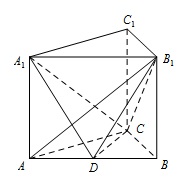

【难度】
【出处】
2012年高考重庆卷(文)
【标注】
-
求异面直线 $ CC_1 $ 和 $ AB $ 的距离;标注答案略解析因为 $ AC=BC $,$ D $ 为 $ AB $ 的中点,故 $ CD\perp AB $.
又在直三棱柱中,$ CC_1\perp $ 平面 $ ABC $,故 $ CC_1\perp CD $,
所以异面直线 $ CC_1 $ 和 $ AB $ 的距离为 $ CD={\sqrt{BC^2-BD^2}}={\sqrt{5}} $. -
若 $ AB_1\perp A_1C $,求二面角 $ A_1-CD-B_1 $ 的平面角的余弦值.标注答案略解析由 $ CD\perp AB$,$CD\perp BB_1$,$AB\cap BB_1=B $,
故 $ CD\perp $ 平面 $ A_1ABB_1 $,
从而 $ CD\perp DA_1$,$ CD\perp DB_1$,
故 $ \angle A_1DB_1 $ 为所求的二面角 $ A_1-CD-B_1 $ 的平面角.
因为 $ A_1D $ 是 $ A_1C $ 在平面 $ A_1ABB_1 $ 上的射影,
又已知 $ AB_1\perp A_1C $,由三垂线定理的逆定理得 $ AB_1\perp A_1D $,
从而 $ \angle A_1AB_1$,$ \angle A_1DA $ 都与 $ \angle B_1AB $ 互余,
因此\[ \angle A_1AB_1=\angle A_1DA ,\]所以 $ {\mathrm{Rt}}\triangle A_1AD\backsim {\mathrm{Rt}}\triangle B_1A_1A $.因此\[ {\dfrac{AA_1}{AD}}={\dfrac{A_1B_1}{AA_1}} ,\]得\[ AA^2_1=AD\cdot A_1B_1=8 ,\]从而\[\begin{split}A_1D&={\sqrt{AA^2_1+AD^2}}=2{\sqrt{3}} ,\\ B_1D&=A_1D=2{\sqrt{3}},\end{split} \]所以在 $ \triangle A_1DB_1 $ 中,由余弦定理得\[ \cos \angle A_1DB_1=\dfrac{{A_1D}^2+B_1D^2-A_1B^2_1}{2\cdot A_1D \cdot B_1D}=\dfrac{1}{3}.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2