如图，在四棱锥 $P - ABCD$ 中，$PA丄$ 平面 $ABCD$，$AC 丄 AD$，$AB 丄 BC$，$\angle BAC = 45^\circ $，$PA = AD = 2$，$AC =1$．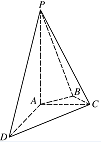
【难度】
【出处】
2012年高考天津卷（理）
【标注】
-
证明 $PC丄 AD$；标注答案略解析解法一：如图，以点 $ A $ 为原点建立空间直角坐标系，
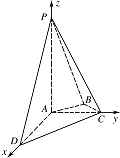依题意得 $ A\left(0,0,0\right),D\left(2,0,0\right),C\left(0,1,0\right),B\left( -{\dfrac{1}{2}},{\dfrac{1}{2}},0\right) ,P\left(0,0,2\right) $．
易得 $ {\overrightarrow {PC}}=\left(0,1,-2\right),{\overrightarrow {AD}}=\left(2,0,0\right)$，
于是 $ {\overrightarrow {PC}}\cdot {\overrightarrow {AD}}=0$，所以 $PC\perp AD$．
解法二：由 $ PA\perp $ 平面 $ ABCD $，可得 $ PA\perp AD $，
又由 $ AD\perp AC $，$ PA\cap AC=A $，则 $ AD\perp $ 平面 $ PAC $，
又 $ PC \subset 平面 PAC $，所以 $ PC\perp AD $． -
求二面角 $A - PC - D$ 的正弦值；标注答案略解析解法一：$ {\overrightarrow {PC}}=\left(0,1,-2\right),{\overrightarrow {CD}}=\left(2,-1,0\right) $．
设平面 $ PCD $ 的法向量 $\overrightarrow n=\left(x,y,z\right) $，则\[ \begin{cases}\overrightarrow n\cdot {\overrightarrow {PC}}=0,\\ \overrightarrow n\cdot {\overrightarrow {CD}}=0,\end{cases} \]即\[ \begin{cases}y-2z=0,\\ 2x-y=0. \end{cases}\]不妨令 $ z=1 $，可得 $ \overrightarrow n=\left(1,2,1\right)$．
可取平面 $ PAC $ 的一个法向量 $\overrightarrow m=\left(1,0,0\right) $，于是\[ \cos \left\langle\overrightarrow m,\overrightarrow n\right\rangle={\dfrac{\overrightarrow m\cdot \overrightarrow n}{ \left|\overrightarrow m \right|\cdot \left|\overrightarrow n \right|}}={\dfrac{{\sqrt{6}}}{6}}, \]从而\[ \sin \left\langle\overrightarrow m,\overrightarrow n\right\rangle ={\dfrac{{\sqrt{30}}}{6}}.\]所以二面角 $ A-PC-D $ 的正弦值为 $ {\dfrac{{\sqrt{30}}}{6}} $．
解法二：如图，作 $ AH\perp PC $ 于点 $ H $，连接 $ DH $．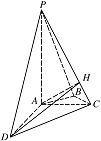
由 $ PC\perp AD $，$ PC\perp AH $，可得 $ PC\perp $ 平面 $ ADH $，
因此 $ DH\perp PC $，从而 $ \angle AHD $ 为二面角 $ A-PC-D $ 的平面角．
在 ${\mathrm{ Rt}}\triangle PAC $ 中，$ PA=2,AC=1 $，由此得 $ AH={\dfrac{2}{{\sqrt{5}}}} $．
由（1）知 $ AD\perp AH $，故在 $ {\mathrm{Rt}}\triangle DAH $ 中，\[ DH={\sqrt{AD^2+AH^2}}={\dfrac{2{\sqrt{30}}}{5}}, \]因此\[ \sin \angle AHD={\dfrac{AD}{DH}}={\dfrac{{\sqrt{30}}}{6}}, \]所以二面角 $ A-PC-D $ 的正弦值为 $ {\dfrac{{\sqrt{30}}}{6}} $． -
设 $E$ 为棱 $PA$ 上的点，满足异面直线 $BE$ 与 $CD$ 所成的角为 $30^\circ $，求 $AE$ 的长．标注答案略解析解法一：设点 $ E $ 的坐标为 $ \left(0,0,h\right) $，其中 $ h\in\left[0,2\right] $，由此得\[ {\overrightarrow {BE}}=\left( {\dfrac{1}{2}},-{\dfrac{1}{2}},h \right). \]由 $ {\overrightarrow {CD}}=\left(2,-1,0\right) $，故\[ \cos \left\langle{\overrightarrow {BE}},{\overrightarrow {CD}}\right\rangle= \dfrac{{\overrightarrow {BE}}\cdot {\overrightarrow {CD}} }{ \left|{\overrightarrow {BE}} \right|\cdot \left|{\overrightarrow {CD}} \right|} ={\dfrac{3}{{\sqrt{10+20h^2}}}}, \]所以\[ {\dfrac{3}{{\sqrt{10+20h^2}}}}=\cos 30^\circ ={\dfrac{{\sqrt{3}}}{2}}, \]解得 $ h={\dfrac{{\sqrt{10}}}{10}}$，即 $AE $ 的长为 ${\dfrac{{\sqrt{10}}}{10}}. $
解法二：如图，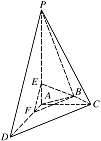
因为 $ \angle ADC<45^\circ $，则过点 $ B $ 作 $ CD $ 的平行线必与线段 $ AD $ 相交，设交点为 $ F $，连接 $ BE,EF $．
则 $ \angle EBF $ 或其补角为异面直线 $ BE $ 与 $ CD $ 所成的角．
由于 $ BF\parallel CD $，则 $ \angle AFB=\angle ADC $．
在 $ {\mathrm{Rt}}\triangle DAC $ 中，\[ CD={\sqrt{5}},\sin \angle ADC={\dfrac{1}{{\sqrt{5}}}}, \]从而\[ \sin \angle AFB={\dfrac{1}{{\sqrt{5}}}}. \]在 $ \triangle AFB $ 中，由正弦定理得\[{\dfrac{BF}{\sin \angle FAB}}={\dfrac{AB}{\sin \angle AFB}},\]由 $AB={\dfrac{1}{{\sqrt{2}}}},\sin \angle FAB=\sin 135^\circ ={\dfrac{{\sqrt{2}}}{2}}, $ 解得 $ BF={\dfrac{{\sqrt{5}}}{2}}$．
由余弦定理，\[ BF^2=AB^2+AF^2-2AB\cdot AF\cdot \cos \angle FAB,\]可得 $ AF={\dfrac{1}{2}}$．
设 $ AE=h $，在 ${\mathrm{ Rt}}\triangle EAF $ 中，\[ EF={\sqrt{AE^2+AF^2}}={\sqrt{h^2+{\dfrac{1}{4}}}}; \]在 $ {\mathrm{Rt}}\triangle BAE $ 中，\[ BE={\sqrt{AE^2+AB^2}}={\sqrt{h^2+{\dfrac{1}{2}}}}. \]在 $ \triangle EBF $ 中，因为 $ EF<BE $，从而 $ \angle EBF=30^\circ $，由余弦定理得\[ \cos 30^\circ ={\dfrac{BE^2+BF^2-EF^2}{2BE\cdot BF}}. \]可解得 $ h={\dfrac{{\sqrt{10}}}{10}}$，所以 $AE $ 的长为 ${\dfrac{{\sqrt{10}}}{10}}. $
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
