查看数据源：59bb3ad477c760000832acb3
如图，四边形 $ABCD$ 有外接圆，已知 $AB=2$，$BC=6$，$CD=DA=4$．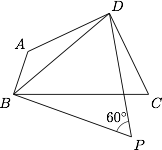
【难度】
【出处】
2015年第二十六届“希望杯”全国数学邀请赛高一（二试）
【标注】
  • 知识点
    >
    三角
    >
    解三角形
    >
    余弦定理
  • 知识点
    >
    三角
    >
    解三角形
    >
    余弦定理
  • 知识点
    >
    不等式
    >
    常用不等式
    >
    均值不等式
  • 方法
    >
    思考方式
    >
    数学建模
  1. 求对角线 $BD$ 的长；
    标注
    • 知识点
      >
      三角
      >
      解三角形
      >
      余弦定理
    答案
    $2\sqrt 7$
    解析
    在 $\triangle{ABD}$ 中，由余弦定理有$$\cos A=\dfrac{16+4-BD^2}{2\cdot 2\cdot 4},$$在 $\triangle{BCD}$ 中，由余弦定理有$$\cos C=\dfrac{36+16-BD^2}{2\cdot 4\cdot 6}.$$依题意有 $\cos A+\cos C=0$，解得 $BD=2\sqrt 7$．
  2. 作 $\angle{BPD=60^{\circ}}$，试求 $PB^2+PD^2$ 的取值范围．
    标注
    • 知识点
      >
      三角
      >
      解三角形
      >
      余弦定理
    • 知识点
      >
      不等式
      >
      常用不等式
      >
      均值不等式
    • 方法
      >
      思考方式
      >
      数学建模
    答案
    $(28,56]$
    解析
    设 $BP=x$，$DP=y$，在 $\triangle{BPD}$ 中，由余弦定理有$$\dfrac 12=\dfrac{x^2+y^2-28}{2xy},$$即 \[x^2+y^2=xy+28>28.\]又$$x^2+y^2=xy+28\leqslant \dfrac{x^2+y^2}{2}+28,$$解得 $x^2+y^2\leqslant 56$，当且仅当 $x=y=2\sqrt 7$ 时等号成立．
    综上所述，所求的取值范围是 $(28,56]$．
题目 问题1 答案1 解析1 备注1 问题2 答案2 解析2 备注2
0.210409s