已知圆锥的母线长为 $l$，底面半径为 $r$，求此圆锥的内接正 $n(n\geqslant3)$ 棱柱的体积的最大值，及对应的 $n$ 棱柱的底面多边形的边长．
【难度】
【出处】
2015年第二十六届“希望杯”全国数学邀请赛高二（二试）
【标注】
【答案】
$\dfrac{2}{27}nr^2\sqrt{l^2-r^2}\cdot\sin\dfrac{2\pi}{n}$，$\dfrac43r\sin\dfrac{\pi}{n}$
【解析】
取过 $n$ 棱柱一个顶点 $A$ 的截面研究，如图．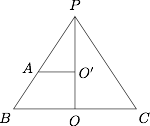
设圆锥高为 $H$，$n$ 棱柱的高为 $h$，边长为 $a$，则$$H=\sqrt{l^2-r^2} , BO=r , AO'=\dfrac{a}{2\sin\dfrac{\pi}{n}}.$$根据 $\triangle PAO'$ 与 $\triangle PBO$ 相似，可得$$\dfrac{H-h}{H}=\dfrac{AO'}{r}=\dfrac{a}{2r\sin\dfrac{\pi}{n}},$$所以\[h=\left(1-\dfrac{a}{2r\sin\dfrac{\pi}{n}}\right)\cdot\sqrt{l^2-r^2},\]$n$ 棱柱的底面面积为\[S=\dfrac{n}{2}\cdot AO'^2\cdot\sin\dfrac{2\pi}{n},\]因此\[\begin{split}V=&\dfrac{n}{2}\cdot\dfrac{a^2}{4\sin^2\dfrac{\pi}{n}}\cdot\sin\dfrac{2\pi}{n}\cdot\left(1-\dfrac{a}{2r\sin\dfrac{\pi}{n}}\right)\cdot\sqrt{l^2-r^2}\\&=2nr^2\sqrt{l^2-r^2}\cdot\sin\dfrac{2\pi}{n}\cdot\dfrac{a}{4r\sin\dfrac{\pi}{n}}\cdot\dfrac{a}{4r\sin\dfrac{\pi}{n}}\cdot\left(1-\dfrac{a}{2r\sin\dfrac{\pi}{n}}\right)\\&\leqslant\dfrac{2}{27}nr^2\sqrt{l^2-r^2}\cdot\sin\dfrac{2\pi}{n}.\end{split}\]当 $a=\dfrac43r\sin\dfrac{\pi}{n}$ 时，取得等号．
设圆锥高为 $H$，$n$ 棱柱的高为 $h$，边长为 $a$，则$$H=\sqrt{l^2-r^2} , BO=r , AO'=\dfrac{a}{2\sin\dfrac{\pi}{n}}.$$根据 $\triangle PAO'$ 与 $\triangle PBO$ 相似，可得$$\dfrac{H-h}{H}=\dfrac{AO'}{r}=\dfrac{a}{2r\sin\dfrac{\pi}{n}},$$所以\[h=\left(1-\dfrac{a}{2r\sin\dfrac{\pi}{n}}\right)\cdot\sqrt{l^2-r^2},\]$n$ 棱柱的底面面积为\[S=\dfrac{n}{2}\cdot AO'^2\cdot\sin\dfrac{2\pi}{n},\]因此\[\begin{split}V=&\dfrac{n}{2}\cdot\dfrac{a^2}{4\sin^2\dfrac{\pi}{n}}\cdot\sin\dfrac{2\pi}{n}\cdot\left(1-\dfrac{a}{2r\sin\dfrac{\pi}{n}}\right)\cdot\sqrt{l^2-r^2}\\&=2nr^2\sqrt{l^2-r^2}\cdot\sin\dfrac{2\pi}{n}\cdot\dfrac{a}{4r\sin\dfrac{\pi}{n}}\cdot\dfrac{a}{4r\sin\dfrac{\pi}{n}}\cdot\left(1-\dfrac{a}{2r\sin\dfrac{\pi}{n}}\right)\\&\leqslant\dfrac{2}{27}nr^2\sqrt{l^2-r^2}\cdot\sin\dfrac{2\pi}{n}.\end{split}\]当 $a=\dfrac43r\sin\dfrac{\pi}{n}$ 时，取得等号．
答案
解析
备注
