如图，在四棱锥 $ P-ABCD $ 中，底面 $ ABCD $ 是矩形，$ AD\perp PD$，$BC=1$，$PC=2{\sqrt{3}}$，$PD=CD=2$．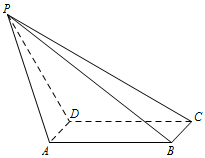
【难度】
【出处】
2012年高考天津卷（文）
【标注】
-
求异面直线 $ PA $ 与 $ BC $ 所成角的正切值；标注答案略解析在四棱锥 $ P-ABCD $ 中，因为底面 $ ABCD $ 是矩形，
所以 $ AD=BC $ 且 $ AD\parallel BC $，
故 $ \angle PAD $ 为异面直线 $ PA $ 与 $ BC $ 所成的角．
在 $ {\mathrm{Rt}}\triangle PDA $ 中，$ \tan \angle PAD={\dfrac{PD}{AD}}=2 $．
所以，异面直线 $ PA $ 与 $ BC $ 所成角的正切值为 $ 2 $． -
证明：平面 $ PDC\perp $ 平面 $ ABCD $；标注答案略解析由于底面 $ ABCD $ 是矩形，
所以 $ AD\perp CD $，
又由于 $ AD\perp PD$，$CD\cap PD=D $，
因此 $ AD\perp $ 平面 $ PDC $，
而 $ AD \subset $ 平面 $ ABCD $，
所以平面 $ PDC\perp $ 平面 $ ABCD $． -
求直线 $ PB $ 与平面 $ ABCD $ 所成角的正弦值．标注答案略解析在平面 $ PDC $ 内，过点 $ P $ 作 $ PE\perp CD $ 交直线 $ CD $ 于点 $ E $，连接 $ EB $．
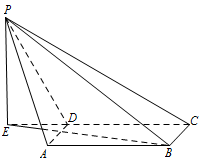由于平面 $ PDC\perp $ 平面 $ ABCD $，而直线 $ CD $ 是平面 $ PDC $ 与平面 $ ABCD $ 的交线，
则 $ PE\perp $ 平面 $ ABCD $，由此得 $ \angle PBE $ 为直线 $ PB $ 与平面 $ ABCD $ 所成的角．
在 $ \triangle PDC $ 中，由于 $ PD=CD=2$，$PC=2{\sqrt{3}} $，可得 $ \angle PCD=30^\circ $．
在 $ {\mathrm{Rt}}\triangle PEC $ 中，$ PE=PC\sin 30^\circ ={\sqrt{3}} $．
由 $ AD\parallel BC$，$AD\perp $ 平面 $ PDC $，得 $ BC\perp $ 平面 $ PDC $，因此 $ BC\perp PC $．
在 $ {\mathrm{Rt}}\triangle PCB $ 中，$ PB={\sqrt{PC^2+BC^2}}={\sqrt{13}} $．
在 $ {\mathrm{Rt}}\triangle PEB $ 中，$ \sin \angle PBE={\dfrac{PE}{PB}}={\dfrac{{\sqrt{39}}}{13}} $．
所以直线 $ PB $ 与平面 $ ABCD $ 所成角的正弦值为 $ {\dfrac{{\sqrt{39}}}{13}} $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
