如图，直三棱柱 $ ABC -A_1B_1C_1 $ 中，$ AC=BC={\dfrac{1}{2}}AA_1 $，$ D $ 是棱 $ AA_1 $ 的中点，$ DC_1\perp BD $．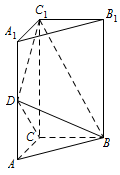
【难度】
【出处】
2012年高考新课标全国卷（理）
【标注】
-
证明：$ DC_1\perp BC $；标注答案略解析由题设知，三棱柱的侧面为矩形．由于 $ D $ 为 $ AA_1 $ 的中点，故 $ DC=DC_1 $．
又 $ AC={\dfrac{1}{2}}AA_1$，可得\[DC^2_1+DC^2=CC^2_1 ,\]所以 $ DC_1\perp DC $．而\[DC_1\perp BD,DC\cap BD=D, \]所以 $ DC_1\perp $ 平面 $ BCD $．又 $ BC \subset$ 平面 $ BCD $，故 $D C_1\perp BC $． -
求二面角 $ A_1 -BD- C_1 $ 的大小．标注答案略解析由（1）知 $ BC\perp DC_1 $，且 $ BC\perp CC_1 $，则 $ BC\perp $ 平面 $ ACC_1 A_1$，
所以 $ CA$，$CB$，$CC_1 $ 两两相互垂直．
以 $ C $ 为坐标原点，$ \overrightarrow {CA} $ 的方向为 $ x $ 轴的正方向，$ \left|\overrightarrow {CA} \right| $ 为单位长，
建立如图所示的空间直角坐标系 $ C-xyz $．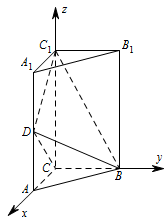
由题意知 $ A_1\left(1,0,2\right)$，$B\left(0,1,0\right)$，$D\left(1,0,1\right)$，$C_1\left(0,0,2\right) $，则\[\overrightarrow {A_1D}=\left(0,0,-1\right),\overrightarrow {BD}=\left(1,-1,1\right),\overrightarrow {DC_1}=\left(-1,0,1\right) ,\]设 $\overrightarrow n=\left(x,y,z\right) $ 是平面 $ A_1B_1BD $ 的法向量，则\[\begin{cases}\overrightarrow n\cdot \overrightarrow {BD}&=0,\\ \overrightarrow n\cdot \overrightarrow {A_1D}&=0,\end{cases} \]即\[\begin{cases} x-y+z=0,\\ z=0,\end{cases}\]可取 $\overrightarrow n=\left(1,1,0\right) $．同理，设 $\overrightarrow m=\left(x_1,y_1,z_1\right) $ 是平面 $ C_1BD $ 的法向量，则\[ \begin{cases}\overrightarrow m\cdot \overrightarrow {BD}=0,\\ \overrightarrow m\cdot \overrightarrow {DC_1}=0 ,\end{cases}\]即\[ \begin{cases}x_1-y_1+z_1=0,\\-x_1+z_1=0, \end{cases}\]可取 $\overrightarrow m=\left(1,2,1\right) $．从而\[ \cos \left \langle \overrightarrow n,\overrightarrow m \right \rangle=\dfrac{\overrightarrow n\cdot \overrightarrow m}{ \left|\overrightarrow n \right|\cdot \left|\overrightarrow m \right|}=\dfrac{\sqrt{3}}{2}. \]故二面角 $ A_1-BD-C_1 $ 的大小为 $ 30^\circ $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
