如图,三棱柱 $ABC - {A_1}{B_1}{C_1}$ 中,侧棱垂直底面,$\angle ACB = 90^\circ $,$AC = BC = \dfrac{1}{2}A{A_1}$,$D$ 是棱 $A{A_1}$ 的中点.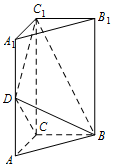

【难度】
【出处】
2012年高考新课标全国卷(文)
【标注】
-
证明:平面 $BD{C_1} \perp $ 平面 $BDC$;标注答案略解析由题设知 $BC \perp C{C_1}$,$BC \perp AC$,$C{C_1} \cap AC = C$,
$\therefore BC \perp $ 平面 $AC{C_1}{A_1}$,
又 $\because D{C_1} \subset $ 平面 $AC{C_1}{A_1}$,$\therefore D{C_1} \perp BC$,
由题设知 $\angle {A_1}D{C_1} = \angle ADC = 45^\circ$,
$\therefore$ $\angle CD{C_1} = 90^\circ $,即 $D{C_1} \perp DC$,
又 $\because DC \cap BC = C$,$\therefore D{C_1} \perp $ 平面 $BDC$,
$\because D{C_1} \subset $ 平面 $BD{C_1}$,$\therefore$ 平面 $BDC_1 \perp $ 平面 $BD{C}$. -
平面 $BD{C_1}$ 分此棱柱为两部分,求这两部分体积的比.标注答案略解析设棱锥 $B - DAC{C_1}$ 的体积为 ${V_1}$,$AC = 1$,由题意得,\[{V_1} = \dfrac{1}{3} \times \dfrac{1 + 2}{2} \times 1 \times 1 = \dfrac{1}{2},\]又三棱柱 $ABC - {A_1}{B_1}{C_1}$ 的体积 $V = 1$,所以\[\left( {V - {V_1}} \right):{V_1} = 1:1,\]$\therefore$ 平面 $BD{C_1}$ 分此棱柱所成两部分体积之比为 $ 1:1 $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2