已知圆 $M:x^2+(y-2)^2=1$，设点 $B,C$ 是直线 $l:x-2y=0$ 上的两点，它们的横坐标分别是 $t,t+4$，点 $P$ 在线段 $BC$ 上，过点 $P$ 作圆 $M$ 的切线 $PA$，切点为 $A$．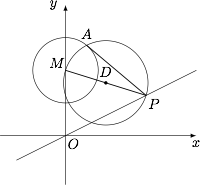
【难度】
【出处】
无
【标注】
-
若 $t=0$，$MP=\sqrt5$，求直线 $PA$ 的方程；标注答案$y=1$ 或 $4x+3y-11=0$解析设 $P(2a,a)$，其中 $a\in [0,2]$，则由 $MP=\sqrt 5$ 可得\[\sqrt{(2a)^2+(a-2)^2}=\sqrt 5,\]解得 $a=1$．进而可设直线\[PA:(x-2)\sin\theta-(y-1)\cos\theta=0,\]由 $PA$ 与圆 $M$ 相切可得\[|-2\sin\theta-\cos\theta|=1,\]解得\[(\sin\theta,\cos\theta)=(0,1),\left(\dfrac 45,-\dfrac 35\right),\]因此直线 $PA$ 的方程是 $y-1=0$ 或 $4x+3y-11=0$．
-
若 $O$ 为原点，经过 $A,P,M$ 三点的圆的圆心是 $D$，求线段 $DO$ 长的最小值 $L(t)$．标注答案$L(t)=\begin{cases} \dfrac14\sqrt{5t^2+8t+16},&t>-\dfrac45,\\
\dfrac{2\sqrt5}{5},&-\dfrac{24}{5}\leqslant t\leqslant -\dfrac45,\\
\dfrac14\sqrt{5t^2+48t+128},&t<-\dfrac{24}{5}. \end{cases}$解析根据题意，$D$ 是线段 $MP$ 的中点，因此 $D$ 点在直线 $l':x-2y+2=0$ 即 $l':y=\dfrac 12x+1$ 上．
又 $P$ 点的横坐标取值范围是 $[t,t+4]$，于是 $D$ 点横坐标的取值范围是 $\left[\dfrac t2,\dfrac t2+2\right]$．过 $O$ 作直线 $l'$ 的垂线，垂足 $H\left(-\dfrac 25,\dfrac 45\right)$．按 $-\dfrac 25$ 与区间 $\left[\dfrac t2,\dfrac t2+2\right]$ 的位置关系进行讨论，记\[\begin{split} m&=\sqrt{\left(\dfrac t2\right)^2+\left(\dfrac t4+1\right)^2}=\dfrac 14\sqrt{5t^2+8t+16},\\
n&=\sqrt{\left(\dfrac t2+2\right)^2+\left(\dfrac t4+2\right)^2}=\dfrac 14\sqrt{5t^2+48t+128},\\
OH&=\sqrt{\left(-\dfrac 25\right)^2+\left(\dfrac 45\right)^2}=\dfrac{2\sqrt 5}5,\end{split}\]有\[L(t)=\begin{cases} m,&-\dfrac 25<\dfrac t2,\\
OH,&\dfrac t2\leqslant -\dfrac 25\leqslant \dfrac t2+2,\\
n,&\dfrac t2+2<-\dfrac 25,\end{cases}\]即\[L(t)=\begin{cases} \dfrac14\sqrt{5t^2+8t+16},&t>-\dfrac45,\\
\dfrac{2\sqrt5}{5},&-\dfrac{24}{5}\leqslant t\leqslant -\dfrac45,\\
\dfrac14\sqrt{5t^2+48t+128},&t<-\dfrac{24}{5}. \end{cases}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
