如图，在侧棱垂直底面的四棱柱 $ ABCD-A_1B_1C_1D_1 $ 中，$ AD\parallel BC$，$AD\perp AB$，$AB={\sqrt{2}}$，$AD=2$，$BC=4$，$AA_1=2$，$ E $ 是 $ DD_1 $ 的中点，$ F $ 是平面 $ B_1C_1E $ 与直线 $ AA_1 $ 的交点．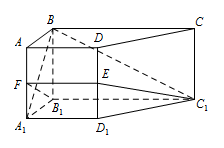
【难度】
【出处】
2012年高考浙江卷（文）
【标注】
-
证明：
（i）$ EF\parallel A_1D_1 $；
（ii）$ BA_1\perp $ 平面 $ B_1C_1EF $；标注答案略解析证明：（i）因为 $ C_1B_1\parallel A_1D_1 $，$ C_1B_1\not\subset 平面 ADD_1A_1 $，
所以 $ C_1B_1\parallel 平面 A_1D_1DA $．
又因为平面 $ B_1C_1EF\cap $ 平面 $ A_1D_1DA=EF $，
所以 $ C_1B_1\parallel EF $，所以 $ A_1D_1\parallel EF $．
（ii）因为 $ BB_1\perp $ 平面 $ A_1B_1C_1D_1 $，所以 $ BB_1\perp B_1C_1 $．
又因为 $ B_1C_1\perp B_1A_1 $，所以 $ B_1C_1\perp $ 平面 $ ABB_1A_1 $，
所以 $ B_1C_1\perp BA_1 $．
在矩形 $ ABB_1A_1 $ 中，$ F $ 是 $ AA_1 $ 的中点，\[ \tan \angle A_1B_1F=\tan \angle AA_1B={\dfrac{{\sqrt{2}}}{2}}, \]即\[ \angle A_1B_1F=\angle AA_1B ,\]故\[ BA_1\perp B_1F .\]所以 $ BA_1\perp $ 平面 $ B_1C_1EF $． -
求 $ BC_1 $ 与平面 $ B_1C_1EF $ 所成的角的正弦值．标注答案略解析如图，设 $ BA_1 $ 与 $ B_1F $ 交点为 $ H $，连接 $ C_1H $，
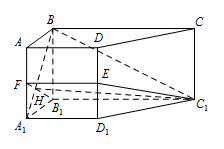由（1）知 $ BA_1\perp $ 平面 $ B_1C_1EF $，
所以 $ \angle BC_1H $ 是 $ BC_1 $ 与平面 $ B_1C_1EF $ 所成的角．
在矩形 $ AA_1B_1B $ 中，$ AB={\sqrt{2}}$，$AA_1=2 $，得 $BH={\dfrac{4}{{\sqrt{6}}}}$．
在直角 $ \triangle BHC_1 $ 中，$ BC_1=2{\sqrt{5}}$，$BH={\dfrac{4}{{\sqrt{6}}}} $，得\[ \sin \angle BC_1H={\dfrac{BH}{BC_1}}={\dfrac{{\sqrt{30}}}{15}}. \]所以 $ BC_1 $ 与平面 $ B_1C_1EF $ 所成角的正弦值是 $ {\dfrac{{\sqrt{30}}}{15}} $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
