如图，在四棱锥 $ P-ABCD $ 中，底面是边长为 $ 2{\sqrt{3}} $ 的菱形，$ \angle BAD=120^\circ $，且 $ PA\perp 平面 ABCD $，$ PA=2{\sqrt{6}}$，$M$，$N $ 分别为 $ PB$，$PD $ 的中点．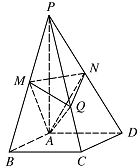
【难度】
【出处】
2012年高考浙江卷（理）
【标注】
-
证明：$ MN\parallel 平面 ABCD $；标注答案略解析连接 $ BD $．因为 $ M$，$N $ 分别是 $ PB$，$PD $ 的中点，所以 $ MN $ 是 $ \triangle PBD $ 的中位线，所以 $ MN\parallel BD $．又因为 $ MN \not\subset 平面 ABCD $，所以 $ MN\parallel 平面 ABCD $．
-
过点 $ A $ 作 $ AQ\perp PC $，垂足为点 $ Q $，求二面角 $ A-MN-Q $ 的平面角的余弦值．标注答案略解析解法一：连接 $ AC $ 交 $ BD $ 于 $ O $，以 $ O $ 为原点，$ OC$，$OD $ 所在直线为 $ x$，$y$ 轴，
建立空间直角坐标系 $ O-xyz $，如图所示．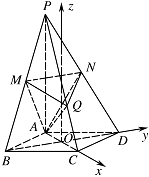
在菱形 $ ABCD $ 中，$ \angle BAD=120^\circ $，得\[ AC=AB=2{\sqrt{3}},BD={\sqrt{3}}AB=6, \]又因为 $ PA\perp 平面 ABCD $，所以 $ PA\perp AC $．在直角 $ \triangle PAC $ 中，\[AC=2{\sqrt{3}},PA=2{\sqrt{6}},AQ\perp PC ,\]得\[QC=2,PQ=4.\]由此知各点坐标如下：\[ A\left(-{\sqrt{3}},0,0\right),B\left(0,-3,0\right),C\left({\sqrt{3}},0,0\right),D\left(0,3,0\right),P\left(-{\sqrt{3}},0,2{\sqrt{6}}\right),\\M \left(-{\dfrac{{\sqrt{3}}}{2}},-{\dfrac{3}{2}}, {\sqrt{6}} \right),N \left(-{\dfrac{{\sqrt{3}}}{2}},{\dfrac{3}{2}}, {\sqrt{6}}\right) ,Q \left({\dfrac{{\sqrt{3}}}{3}},0,{\dfrac{2{\sqrt{6}}}{3}} \right). \]设 $\overrightarrow m=\left(x,y,z\right) $ 为平面 $ AMN $ 的法向量．由\[ \overrightarrow {AM}=\left( \dfrac{\sqrt{3}}{2},-\dfrac{3}{2}, \sqrt{6}\right) ,\overrightarrow {AN}= \left(\dfrac{{\sqrt{3}}}{2},\dfrac{3}{2}, \sqrt{6} \right)\]知\[ \begin{cases} \dfrac{\sqrt 3}{2}x-\dfrac{3}{2}y+{\sqrt{6}}z=0,\\ \dfrac{\sqrt 3}{2}x+\dfrac{3}{2}y+\sqrt{6}z=0, \end{cases}\]取 $ z=-1 $，得 $\overrightarrow m=\left(2{\sqrt{2}},0,-1\right) $．
设 $ \overrightarrow n=\left(x_1,y_1,z_1\right) $ 为平面 $ QMN $ 的法向量．由\[ {\overrightarrow {QM}}= \left(-{\dfrac{5{\sqrt{3}}}{6}},-{\dfrac{3}{2}},{\dfrac{{\sqrt{6}}}{3}} \right),{\overrightarrow {QN}}= \left(-{\dfrac{5{\sqrt{3}}}{6}},{\dfrac{3}{2}},{\dfrac{{\sqrt{6}}}{3}}\right) \]知\[ \begin{cases}-{\dfrac{5{\sqrt{3}}}{6}}x_1-{\dfrac{3}{2}}y_1+{\dfrac{{\sqrt{6}}}{3}}z_1=0,\\-{\dfrac{5{\sqrt{3}}}{6}}x_1+{\dfrac{3}{2}}y_1+{\dfrac{{\sqrt{6}}}{3}}z_1=0, \end{cases}\]取 $ z_1=5 $，得 $\overrightarrow n=\left(2{\sqrt{2}},0,5\right) $，于是\[ \cos \left \langle \overrightarrow m,\overrightarrow n \right \rangle=\dfrac{\overrightarrow m\cdot \overrightarrow n}{ \left|\overrightarrow m \right|\cdot \left|\overrightarrow n \right|}=\dfrac{\sqrt{33}}{33} ,\]所以二面角 $ A-MN-Q $ 的平面角的余弦值为 $ {\dfrac{{\sqrt{33}}}{33}} $．
解法二：如图，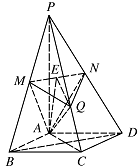
在菱形 $ ABCD $ 中，$ \angle BAD=120^\circ $，得\[\begin{split} AC&=AB=BC=CD=DA,\\BD&={\sqrt{3}}AB,\end{split} \]又因为 $ PA\perp 平面 ABCD $，所以\[ PA\perp AB,PA\perp AC,PA\perp AD ,\]所以\[ PB=PC=PD ,\]所以\[ \triangle PBC\cong \triangle PDC.\]而 $ M$，$N $ 分别是 $ PB$，$PD $ 的中点，所以\[ MQ=NQ ,\]且\[ AM={\dfrac{1}{2}}PB={\dfrac{1}{2}}PD=AN ,\]取线段 $ MN $ 的中点 $ E $，连接 $ AE$，$EQ $，则\[ AE\perp MN,QE\perp MN, \]所以 $ \angle AEQ $ 为二面角 $ A-MN-Q $ 的平面角．
由 $ AB=2{\sqrt{3}}$，$PA=2{\sqrt{6}} $，故在 $ \triangle AMN $ 中，\[ AM=AN=3,MN={\dfrac{1}{2}}BD=3,\]得\[ AE={\dfrac{3{\sqrt{3}}}{2}} .\]在直角 $ \triangle PAC $ 中，\[ AQ\perp PC ,\]得\[AQ=2{\sqrt{2}} ,QC=2,PQ=4.\]在 $ \triangle PBC $ 中，\[\cos \angle BPC={\dfrac{PB^2+PC^2-BC^2}{2PB\cdot PC}}={\dfrac{5}{6}} ,\]得\[ MQ={\sqrt{PM^2+PQ^2-2PM\cdot PQ\cos \angle BPC}}={\sqrt{5}}. \]在等腰 $ \triangle MQN $ 中，\[ MQ=NQ={\sqrt{5}},MN=3 ,\]得\[ QE={\sqrt{MQ^2-ME^2}}={\dfrac{{\sqrt{11}}}{2}}, \]在 $ \triangle AEQ $ 中，\[ AE={\dfrac{3{\sqrt{3}}}{2}},QE={\dfrac{{\sqrt{11}}}{2}},AQ=2{\sqrt{2}} ,\]得\[ \cos \angle AEQ={\dfrac{AE^2+QE^2-AQ^2}{2AE\cdot QE}}={\dfrac{{\sqrt{33}}}{33}}, \]所以二面角 $ A-MN-Q $ 的平面角的余弦值为 $ {\dfrac{{\sqrt{33}}}{33}} $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
