如图,在正四棱柱 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 中,$A{A_1} = 2$,$AB = 1$,点 $N$ 是 $BC$ 的中点,点 $M$ 在 $C{C_1}$ 上.设二面角 ${A_1} - DN - M$ 的大小为 $\theta $.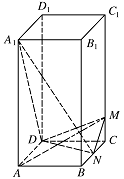

【难度】
【出处】
2011年高考江苏卷
【标注】
-
当 $\theta = 90^\circ $ 时,求 $AM$ 的长;标注答案略解析以 $D$ 为原点,$DA$ 为 $x$ 轴正半轴,$DC$ 为 $y$ 轴正半轴,$D{D_1}$ 为 $z$ 轴正半轴,建立空间直角坐标系.
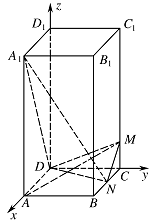 则 $A\left( {1,0,0} \right),$ ${A_1}\left( {1,0,2} \right)$,$N\left( {\dfrac{1}{2},1,0} \right)$,$C\left( {0,1,0} \right)$.
则 $A\left( {1,0,0} \right),$ ${A_1}\left( {1,0,2} \right)$,$N\left( {\dfrac{1}{2},1,0} \right)$,$C\left( {0,1,0} \right)$.
设 $M\left( {0,1,t} \right)$,面 $MDN$ 的法向量 $\overrightarrow {m} = \left( {{x_1},{y_1},{z_1}} \right)$,则\[\left\{ \begin{gathered}
\overrightarrow m \cdot \overrightarrow {DN} = 0, \\
\overrightarrow m \cdot \overrightarrow {DM} = 0, \\
\end{gathered} \right.\]即\[\left\{ \begin{gathered}{x_1} + 2{y_1} = 0, \\
{y_1} + tz = 0, \\
\end{gathered} \right.\]取 $x_1=2t $,则\[\overrightarrow m = \left( {2t, - t,1} \right).\]设面 ${A_1}DN$ 的法向量为 $\overrightarrow n = \left( {{x_0},{y_0},{z_0}} \right)$,则\[\begin{cases}\overrightarrow {D{A_1}} \cdot \overrightarrow n = 0,\\ \overrightarrow {DN} \cdot \overrightarrow n = 0, \end{cases}\]即\[\begin{cases}{{x_0} + 2{z_0} = 0}, \\
{{x_0} + 2{y_0} = 0},
\end{cases}\]取 ${x_0} = 2,$ 则\[\overrightarrow n = \left( {2, - 1, - 1} \right),\]由题意得\[\overrightarrow m \cdot \overrightarrow n = 5t - 1 = 0, \]解得\[t=\dfrac 15. \]从而\[M\left(0,1,\dfrac 15\right), \]所以\[\begin{split}AM & = \sqrt {{{\left(1 - 0\right)}^2} + {{\left(0 - 1\right)}^2} + {{\left(0 - \dfrac{1}{5}\right)}^2}} \\& = \dfrac{{\sqrt {51} }}{5}.\end{split}\] -
当 $\cos \theta = \dfrac{\sqrt 6 }{6}$ 时,求 $CM$ 的长.标注答案略解析由题意得\[\dfrac{{\left| {\overrightarrow m \cdot \overrightarrow n } \right|}}{{\left| {\overrightarrow m } \right| \cdot \left| {\overrightarrow n } \right|}} = \dfrac{{\left| { 5t -1} \right|}}{{\sqrt 6 \cdot \sqrt {5{t^2} + 1} }} = \dfrac{\sqrt 6 }{6},\]解得\[t=\dfrac 12,t=0\left(舍\right).\]从而 $CM$ 的长为 $ \dfrac{1}{2}.$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2