如图，圆 ${O_1}$ 与圆 ${O_2}$ 内切于点 $A$，其半径分别为 ${r_1}$ 与 ${r_2}$ $\left({r_1} > {r_2}\right)$，圆 ${O_1}$ 的弦 $AB$ 交圆 ${O_2}$ 于点 $C$（${O_1}$ 不在 $AB$ 上），求证：$AB:AC$ 为定值．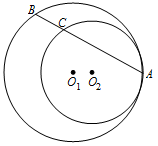
【难度】
【出处】
2011年高考江苏卷
【标注】
-
标注答案略解析如图，连结 $AO_1 $，$BO_1 $，$CO_2 $．
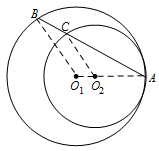由弦切角定理可得 $\triangle A{O_2}C \sim \triangle A{O_1}B$，所以\[\dfrac{{AB}}{{AC}} = \dfrac{{{O_1}B}}{{{O_2}C}} = \dfrac{{{r_1}}}{{{r_2}}}.\]所以 $AB:AC$ 为定值．
题目
问题1
答案1
解析1
备注1
