如图,在平面直角坐标系 $xOy$ 中,$M,N$ 分别是椭圆 $\dfrac{{{x^2}}}{4} + \dfrac{{{y^2}}}{2} = 1$ 的顶点,过坐标原点的直线交椭圆于 $P,A$ 两点,其中点 $P$ 在第一象限,过 $P$ 作 $x$ 轴的垂线,垂足为 $C$,连接 $AC$,并延长交椭圆于点 $B$,设直线 $PA$ 的斜率为 $k$.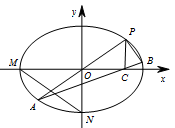

【难度】
【出处】
2011年高考江苏卷
【标注】
-
当直线 $PA$ 平分线段 $MN$ 时,求 $k$ 的值;标注答案略解析依题意可得 $a = 2,b = \sqrt 2$,则\[M\left( { - 2,0} \right) , N\left( {0, - \sqrt 2 } \right),\]$M,N$ 的中点坐标为 $\left( { - 1, - \dfrac{{\sqrt 2 }}{2}} \right)$,所以 $k = \dfrac{{\sqrt 2 }}{2}$.
-
当 $k = 2$ 时,求点 $P$ 到直线 $AB$ 的距离 $d$;标注答案略解析由\[\begin{cases}
y = 2x ,\\
{x^2} + 2{y^2} = 4 ,\\
\end{cases}\]得\[P\left( {\dfrac{2}{3},\dfrac{4}{3}} \right),A\left( { - \dfrac{2}{3}, - \dfrac{4}{3}} \right) , C\left( {\dfrac{2}{3},0} \right),\]$AC$ 方程为\[\dfrac{y}{{ - \dfrac{4}{3}}} = \dfrac{{x - \dfrac{2}{3}}}{{ - \dfrac{2}{3} - \dfrac{2}{3}}},\]即 $y = x - \dfrac{2}{3}$.所以点 $P$ 到直线 $AB$ 的距离\[d = \dfrac{{\left| {\dfrac{2}{3} - \dfrac{4}{3} - \dfrac{2}{3}} \right|}}{{\sqrt 2 }} = \dfrac{{2\sqrt 2 }}{3}.\] -
对任意 $k > 0$,求证:$PA \perp PB$.标注答案略解析由题意设 $P\left({x_0},{y_0}\right),A\left( - {x_0}, - {y_0}\right),B\left({x_1},{y_1}\right)$,则 $C\left({x_0},0\right)$,
$\because$ $A,C,B$ 三点共线,所以\[\dfrac{{{y_1}}}{{{x_1} - {x_0}}} = \dfrac{{{y_0}}}{{2{x_0}}} = \dfrac{{{y_1} + {y_0}}}{{{x_1} + {x_0}}},\]又因为点 $P,B$ 在椭圆上,所以\[\begin{split}\dfrac{{{x_0}^2}}{4} + \dfrac{{{y_0}^2}}{2} & = 1, \dfrac{{{x_1}^2}}{4} + \dfrac{{{y_1}^2}}{2} & = 1,\end{split}\]两式相减得:\[{k_{PB}} = - \dfrac{{{x_0} + {x_1}}}{{2\left({y_0} + {y_1}\right)}},\]所以\[\begin{split}{k_{PA}}{k_{PB}} & = \dfrac{{{y_0}}}{{{x_0}}}\left[ { - \dfrac{{{x_0} + {x_1}}}{{2\left({y_0} + {y_1}\right)}}} \right] = - \dfrac{{\left({y_1} + {y_0}\right)\left({x_0} + {x_1}\right)}}{{\left({x_1} + {x_0}\right)\left({y_0} + {y_1}\right)}} = - 1,\end{split}\]$\therefore$ $PA \perp PB$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3