如图,在四棱锥 $P - ABCD$ 中,平面 $PAD \perp $ 平面 $ABCD$,$AB = AD$,$\angle BAD = 60^\circ $,$E,F$ 分别是 $AP,AD$ 的中点.求证: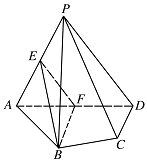

【难度】
【出处】
2011年高考江苏卷
【标注】
-
直线 $EF\parallel $ 平面 $PCD$;标注答案略解析利用线线平行证明线面平行.因为 $E,F$ 分别是 $AP,AD$ 的中点,
$\therefore$ $EF\parallel PD,$
又 $\because$ $P,D \in $ 面 $PCD,E ,F\notin $ 面 $PCD$,
$\therefore$ 直线 $EF\parallel $ 平面 $PCD$. -
平面 $BEF \perp $ 平面 $PAD$.标注答案略解析证明面面垂直的思想是证明一个面上的一条直线垂直于另一个平面.$\because$ $AB = AD,\angle BAD = 60^\circ ,$ $ F $ 是 $AD$ 的中点,
$\therefore$ $BF \perp AD$.
又平面 $PAD \perp $ 平面 $ABCD$,面 $PAD \cap $ 面 $ABCD = AD$,
$\therefore$ $BF \perp $ 面 $PAD$,
又 $ BF\subset $ 面 $BEF$,
$\therefore$ 平面 $BEF \perp $ 平面 $PAD$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2