请你设计一个包装盒,如图所示,$ABCD$ 是边长为 $60{\rm{cm}} $ 的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得 $A,B,C,D$ 四个点重合于图中的点 $P$,正好形成一个正四棱柱形状的包装盒,$E,F$ 在 $AB$ 上,是被切去的等腰直角三角形斜边的两个端点,设 $AE = FB = x$ ${(\rm{cm})} $.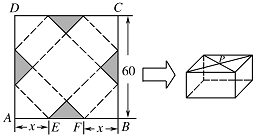

【难度】
【出处】
2011年高考江苏卷
【标注】
-
若广告商要求包装盒侧面积 $S\left( {{{\rm{cm} }^2}} \right)$ 最大,试问 $x$ 应取何值?标注答案略解析\[\begin{split}S & = {60^2} - 4{x^2} - {\left( {60 - 2x} \right)^2} \\& = 240x - 8{x^2} \left( {0 < x < 30} \right),\end{split}\]所以 $x = 15{\rm{cm}} $ 时侧面积最大.
-
若广告商要求包装盒容积 $V\left( {{{\rm{cm} }^3}} \right)$ 最大,试问 $x$ 应取何值?并求出此时包装盒的高与底面边长的比值.标注答案略解析\[\begin{split}V & = {\left( {\sqrt 2x} \right)^2} \cdot \dfrac{{\sqrt 2 }}{2} \cdot \left( {60 - 2x} \right) \\& = 2\sqrt 2 {x^2}\left( {30 - x} \right)\left( {0 < x < 30} \right),\end{split}\]所以,\[V' = 6\sqrt 2 x\left( {20 - x} \right),\]当 $0 < x < 20$ 时,$V$ 递增,
当 $20 < x < 30$ 时,$V$ 递减,
所以,当 $x = 20$ 时,$V$ 最大.
此时,包装盒的高与底面边长的比值为\[\dfrac{{\dfrac{{\sqrt 2 }}{2}\left( {60-2x} \right)}}{{\sqrt 2 x}} = \dfrac{1}{2}.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2