设正实数 $a$，$b$，$c$ 满足 $\begin{cases}a^2+b^2=3,\\ a^2+c^2+ac=4,\\ b^2+c^2+\sqrt 3 bc=7,\end{cases}$ 求 $a$，$b$，$c$ 的值．
【难度】
【出处】
2014年浙江省高中数学竞赛
【标注】
【答案】
$(a,b,c)=\left(\dfrac {6}{37}\sqrt {37},\dfrac {5}{37}\sqrt {111},\dfrac {8}{37}\sqrt {37}\right)$
【解析】
如图，以 $O$ 为出发点，作长度为 $a$，$b$，$c$ 的三条线段 $OA$，$OB$，$OC$，使得 $\angle AOB=90^{\circ}$，$\angle AOC=120^{\circ}$．
由已知条件：$\angle COB=150^{\circ}$．
由余弦定理知$$AB=\sqrt {a^2+b^2}=\sqrt 3 , AC=2 , BC=\sqrt 7,$$于是 $\angle CAB=90^{\circ}$．
过 $O$ 作 $OE\perp AC$，$OF\perp AB$．设 $AE=m$，$OE=n$．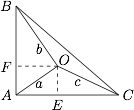
因为 $\angle ABO= \angle OAE $，所以 $\dfrac {OF}{BF}=\dfrac {OE}{AE}$，即$$\dfrac {n}{m}=\dfrac {m}{\sqrt 3-n}.$$又 $\angle AOC=120^{\circ}$，所以 $\tan \angle AOC=-\sqrt 3$，即$$\dfrac {\dfrac mn+\dfrac {2-m}{n}}{1-\dfrac mn\cdot \dfrac {2-m}{n}}=-\sqrt 3,$$于是可得$$\begin{cases}m=\dfrac {30}{37},\\ n =\dfrac {12}{37}\sqrt 3,\end{cases}$$所以$$\begin{cases}a=\dfrac {6}{37}\sqrt {37},\\ b=\dfrac {5}{37}\sqrt {111},\\ c=\dfrac {8}{37}\sqrt {37}.\end{cases}$$
由已知条件：$\angle COB=150^{\circ}$．
由余弦定理知$$AB=\sqrt {a^2+b^2}=\sqrt 3 , AC=2 , BC=\sqrt 7,$$于是 $\angle CAB=90^{\circ}$．
过 $O$ 作 $OE\perp AC$，$OF\perp AB$．设 $AE=m$，$OE=n$．
因为 $\angle ABO= \angle OAE $，所以 $\dfrac {OF}{BF}=\dfrac {OE}{AE}$，即$$\dfrac {n}{m}=\dfrac {m}{\sqrt 3-n}.$$又 $\angle AOC=120^{\circ}$，所以 $\tan \angle AOC=-\sqrt 3$，即$$\dfrac {\dfrac mn+\dfrac {2-m}{n}}{1-\dfrac mn\cdot \dfrac {2-m}{n}}=-\sqrt 3,$$于是可得$$\begin{cases}m=\dfrac {30}{37},\\ n =\dfrac {12}{37}\sqrt 3,\end{cases}$$所以$$\begin{cases}a=\dfrac {6}{37}\sqrt {37},\\ b=\dfrac {5}{37}\sqrt {111},\\ c=\dfrac {8}{37}\sqrt {37}.\end{cases}$$
答案
解析
备注
