如图，在四棱台 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 中，${D_1}D \perp $ 平面 $ABCD$，底面 $ABCD$ 是平行四边形，$AB = 2AD$，$AD = {A_1}{B_1}$，$\angle BAD = 60^\circ $．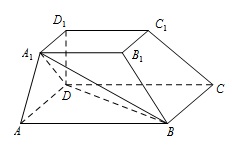
【难度】
【出处】
2011年高考山东卷（文）
【标注】
-
证明：$A{A_1} \perp BD$；标注答案略解析因为 $AB = 2AD$，所以设 $AD = a$，则 $AB = 2a$，
又因为 $\angle BAD = 60^\circ $，所以在 $\triangle ABD$ 中，由余弦定理得：\[{BD}^2 = {\left(2a\right)^2} + {a^2} - 2a \times 2a \times \cos 60^\circ = 3{a^2},\]所以 $BD = \sqrt 3 a$，所以\[{AD} ^2+ {BD}^2 = {AB}^2,\]故 $BD \perp AD$，又因为 ${D_1}D \perp $ 平面 $ABCD$，所以 ${D_1}D \perp BD$，
又因为 $AD \cap {D_1}D = D$，所以 $BD \perp $ 平面 $AD{D_1}{A_1}$，故 $A{A_1} \perp BD$． -
证明：$C{C_1}$ $\parallel $ 平面 ${A_1}BD$．标注答案略解析如图，连接 $AC$，设 $AC \cap BD = O$，连接 ${A_1}O$，
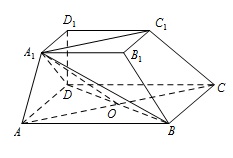由底面 $ABCD$ 是平行四边形得，$O$ 是 $AC$ 的中点，
由四棱台 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 知，平面 $ABCD\parallel $ 平面 ${A_1}{B_1}{C_1}{D_1}$，
因为这两个平面同时都和平面 $AC{C_1}{A_1}$ 相交，交线分别为 $AC,{A_1}{C_1}$，故 $AC\parallel {A_1}{C_1}$，
又因为\[AB = 2a,BC = a,\angle ABC = 120^\circ ,\]所以可由余弦定理计算得\[AC = \sqrt 7 a,\]又因为\[{A_1}{B_1} = a,{B_1}{C_1} = \dfrac{a }{2},\angle {A_1}{B_1}{C_1} = 120^\circ,\]所以可由余弦定理计算得\[{A_1}{C_1} = \dfrac{\sqrt 7 }{2}a,\]所以 ${A_1}{C_1}\parallel OC$ 且 ${A_1}{C_1} = OC$，故四边形 $OC{C_1}{A_1}$ 是平行四边形，所以 $C{C_1}\parallel {A_1}O$，
又 $C{C_1} \not\subset $ 平面 ${A_1}BD$，${A_1}O \subset $ 平面 ${A_1}BD$，所以 $C{C_1}$ $\parallel $ 平面 ${A_1}BD$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
