在平面直角坐标系 $xOy$ 中,已知椭圆 $C:\dfrac{{{x^2}}}{3} + {y^2} = 1$.如图所示,斜率为 $k\left(k > 0\right)$ 且不过原点的直线 $l$ 交椭圆 $C$ 于 $A$,$B$ 两点,线段 $AB$ 的中点为 $E$,射线 $OE$ 交椭圆 $C$ 于点 $G$,交直线 $x = - 3$ 于点 $D\left( - 3,m\right)$.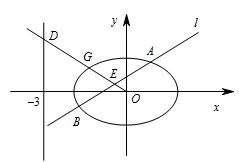

【难度】
【出处】
2011年高考山东卷(文)
【标注】
-
求 ${m^2} + {k^2}$ 的最小值;标注答案略解析由题意,设直线 $l:y = kx + n\left(n> 0\right)$,由\[\begin{cases}y = kx + n ,\\
\dfrac{{{x^2}}}{3} + {y^2} = 1 ,\\
\end{cases}\]消 $y$ 得\[\left(1 + 3{k^2}\right){x^2} + 6knx + 3{n^2} - 3 = 0,\]设 $A\left({x_1},{y_1}\right) , B\left({x_2},{y_2}\right)$,$AB$ 的中点 $E\left({x_0},{y_0}\right)$,则由韦达定理得:\[{x_1} + {x_2} = \dfrac{{ - 6kn}}{{1 + 3{k^2}}},y_1+y_2=\dfrac{2n}{3k^2+1};\]即可得出\[\begin{split}{x_0} & = \dfrac{{ - 3kn}}{{1 + 3{k^2}}} , \\ {y_0} &= \dfrac{n}{{1 + 3{k^2}}},\end{split}\]所以中点 $E$ 的坐标为 $\left( {\dfrac{{ - 3kn}}{{1 + 3{k^2}}},\dfrac{n}{{1 + 3{k^2}}}} \right)$,因为 $O$,$E$,$D$ 三点在同一直线上,所以\[{k_{OE}} = {k_{OD}},\]即\[ - \dfrac{1}{{3k}} = - \dfrac{m}{3},\]解得 $m = \dfrac{1}{k}$,所以\[{m^2} + {k^2} = \dfrac{1}{{{k^2}}} + {k^2} \geqslant 2,\]当且仅当 $k = 1$ 时取等号,即 ${m^2} + {k^2}$ 的最小值为 $2$. -
若 $|OG|^2 = |OD| \cdot |OE|$,
(i)求证:直线 $l$ 过定点;
(ii)试问点 $B$,$G$ 能否关于 $x$ 轴对称?若能,求出此时 $\triangle ABG$ 的外接圆方程;若不能,请说明理由.标注答案略解析(i)由题意知,$n > 0$,因为直线 $OD$ 的方程为 $y = - \dfrac{m}{3}x$,所以由\[\begin{cases}
y = - \dfrac{m}{3}x, \\
\dfrac{{{x^2}}}{3} + {y^2} = 1, \\
\end{cases}\]得交点 $G$ 的纵坐标为\[{y_G} = \sqrt {\dfrac{{{m^2}}}{{{m^2} + 3}}} ,\]又因为 ${y_E} = \dfrac{n}{{1 + 3{k^2}}}$,${y_D} = m$,且 $|OG{|^2} = |OD| \cdot |OE|$,所以\[\dfrac{{{m^2}}}{{{m^2} + 3}} = m \cdot \dfrac{n}{{1 + 3{k^2}}},\]又由(1)知,$m = \dfrac{1}{k}$,所以解得 $k = n$,所以直线 $l$ 的方程为 $l:y = kx + k$,即有\[l:y = k\left(x + 1\right),\]令 $x = - 1$,得 $y = 0$,与实数 $k$ 无关,所以直线 $l$ 过定点 $\left( - 1,0\right)$.
(ii)假设点 $B$,$G$ 关于 $x$ 轴对称,则有 $\triangle ABG$ 的外接圆的圆心在 $x$ 轴上,又在线段 $AB$ 的中垂线上,
由(i)知点 $G\left( {\dfrac{{ - 3}}{{\sqrt {{m^2} + 3} }},\dfrac{m}{{\sqrt {{m^2} + 3} }}} \right)$,所以点 $B\left( {\dfrac{{ - 3}}{{\sqrt {{m^2} + 3} }},\dfrac{{ - m}}{{\sqrt {{m^2} + 3} }}} \right)$,
又因为直线 $l$ 过定点 $\left( - 1,0\right)$,所以直线 $l$ 的斜率为\[\dfrac{{\dfrac{{ - m}}{{\sqrt {{m^2} + 3} }}}}{{\dfrac{{ - 3}}{{\sqrt {{m^2} + 3} }} + 1}} = k,\]又因为 $m = \dfrac{1}{k}$,所以解得\[{m^2} = 1 或 6,\]又因为 $3 - {m^2} > 0$,所以 ${m^2} = 6$ 舍去,即\[{m^2} = 1,\]此时\[k = 1,m = 1,E\left( {\dfrac{{ - 3}}{4},\dfrac{1}{4}} \right),\]$AB$ 的中垂线为\[2x + 2y + 1 = 0,\]圆心坐标为 $\left( { - \dfrac{1}{2},0} \right)$,$G\left( {\dfrac{{ - 3}}{2},\dfrac{1}{2}} \right)$,圆半径为 $\dfrac{{\sqrt 5 }}{2}$,圆的方程为\[{\left( {x + \dfrac{1}{2}} \right)^2} + {y^2} = \dfrac{5}{4}.\]综上所述,点 $B$,$G$ 关于 $x$ 轴对称,此时 $\triangle ABG$ 的外接圆的方程为\[{\left( {x + \dfrac{1}{2}} \right)^2} + {y^2} = \dfrac{5}{4}.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2