题目 已知 $a>b>0$，$a^b=b^a$． 问题1 求证：$a>{\rm e}>b>1$； 答案1 略 解析1 根据题意，有 $\dfrac{\ln a}a=\dfrac{\ln b}b$．<br/>令 $f(x)=\dfrac{\ln x}{x}$，则其导函数\[f'(x)=\dfrac{1}{x^2}\cdot \left(1-\ln x\right),\]于是 $f(x)$ 在 $(0,{\rm e})$ 上单调递增，在 $({\rm e},+\infty)$ 上单调递减，在 $x={\rm e}$ 处取得极大值 $\dfrac{1}{\rm e}$，如图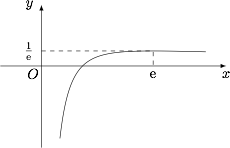．<img src="/static/images/286bf37aaf740f48381f98a8bae882d6.png" class="img-responsive" />因此可得 $a>{\rm e}>b>1$． 备注1 问题2 求证：$a+b>2{\rm e}$； 答案2 略 解析2 显然只需要证明 $a<2{\rm e}$ 的情形，即证明 $b>2{\rm e}-a$，考虑到 $b,2{\rm e}-a$ 均位于 $f(x)$ 的单调递增区间 $(0,{\rm e})$，因此只需要证明\[f(b)>f(2{\rm e}-a),\]也即\[f(a)>f(2{\rm e}-a).\]接下来我们证明\[\forall x \in ({\rm e},2{\rm e}),f(x)-f(2{\rm e}-x)>0.\]设上述不等式左侧为 $g(x)$，则其导函数\[\begin{split}g'(x)&=f'(x)+f'(2{\rm e}-x)\\<br/>&=\dfrac{1-\ln x}{x^2}+\dfrac{1-\ln (2{\rm e}-x)}{(2{\rm e}-x)^2}\\<br/>&=\dfrac{1-\ln (2{\rm e}-x)}{(2{\rm e}-x)^2}-\dfrac{\ln x-1}{x^2}.\end{split}\]考虑到当 $x \in ({\rm e},2{\rm e})$ 时，有\[\ln x+\ln (2{\rm e}-x)=\ln [x\cdot (2{\rm e}-x)]<\ln{\rm e}^2=2,\]于是\[1-\ln (2{\rm e}-x)>\ln x-1>0,\]又当 $x \in ({\rm e},2{\rm e})$ 时，有\[(2{\rm e}-x)^2<x^2,\]于是当 $x \in ({\rm e},2{\rm e})$ 时，有 $g'(x)>0$，因此 $g(x)$ 在 $({\rm e},2{\rm e})$ 上单调递增，结合 $g({\rm e})=0$，命题得证． 备注2 问题3 求证：$a\cdot b>{\rm e}^2$． 答案3 略 解析3 显然只需要证明 $a<{\rm e}^2$ 的情形，与 $(2)$ 类似，只需要证明\[\forall x>{\rm e},f(x)-f\left(\dfrac{{\rm e}^2}{x}\right)>0.\]设上述不等式左侧为 $h(x)$，则其导函数\[\begin{split}<br/>h'(x)&=f'(x)+\dfrac{{\rm e}^2}{x^2}\cdot f'\left(\dfrac{{\rm e}^2}{x}\right)\\<br/>&=\dfrac{1-\ln x}{x^2}+\dfrac{\ln x-1}{x}\\<br/>&=\dfrac{x-1}{x^2}\cdot (\ln x-1)\\<br/>&>0,<br/>\end{split}\]因此 $h(x)$ 在 $({\rm e},{\rm e}^2)$ 上单调递增，结合 $h({\rm e})=0$，命题得证． 备注3 每日一题[825]对称化构造．