已知点 $P(a,b)$（$ab\ne 0$）是圆 $O:x^2+y^2=r^2$ 上的一个已知点，过点 $P$ 作倾斜角互补的两条直线分别于圆 $O$ 交于另外的点 $A$ 和 $B$．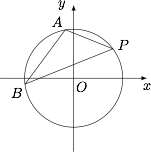
【难度】
【出处】
无
【标注】
-
判断直线 $AB$ 的斜率是否为定值，若是定值，求出该定值；标注答案直线 $AB$ 的斜率为定值 $\dfrac ab$解析如图，作 $P$ 关于 $y$ 轴的对称点 $Q(-a,b)$，$QR$ 为圆 $O$ 的直径．
根据题意，有 $\angle APQ=\angle BPQ$，于是弧 $AQ$ 与弧 $BQ$ 相等，进而由圆的垂径定理可得 $OQ\perp AB$，因此直线 $AB$ 的斜率为定值 $\dfrac ab$． -
求圆的弦 $AB$ 的中点的轨迹方程．标注答案$bx+ay=0,x\in [-|a|,|a|],x\ne \dfrac{a-b}2$解析根据第 $(1)$ 小题的结果可知弦 $AB$ 的中点 $M$ 在直径 $QR$ 上，且 $MP$ 的斜率不为 $\dfrac ab$，因此所求的轨迹方程为\[bx+ay=0,x\in [-|a|,|a|],x\ne \dfrac{a-b}2.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
