如图，在 $\triangle ABC $ 中，$\angle B = \dfrac {\mathrm \pi } 2 $，$AB=BC=2$，$P$ 为 $AB$ 边上一动点，$PD \parallel BC $ 交 $AC$ 于点 $D$，现将 $\triangle PDA$ 沿 $ PD$ 翻折至 $\triangle PDA'$，使 $平面 PDA' \perp 平面 PBCD$．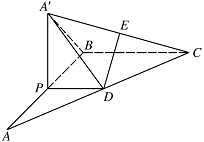
【难度】
【出处】
2011年高考江西卷（文）
【标注】
-
当棱锥 $A'-PBCD$ 的体积最大时，求 $ PA $ 的长；标注答案略解析设 $PA = x$，则\[ {V_{A' - PBCD}} = \dfrac{1}{3}PA \cdot {S_{底面PDCB}} = \dfrac{1}{3}x\left(2 - \dfrac{x^2}{2}\right) . \]令\[ f\left(x\right) = \dfrac{1}{3}x\left(2 - \dfrac{x^2}{2}\right) = \dfrac{2x}{3} - \dfrac{x^3}{6},\left(0<x<2\right) , \]则\[f'\left(x\right) = \dfrac{2}{3} - \dfrac{x^2}{2},\]由 $ f'\left(x\right)=0$，得 $x=\dfrac {2\sqrt 3 } 3 $（负值舍去）．\[\begin{array}{|c|c|c|c|} \hline
x & \left(0,\frac{2\sqrt 3}{3}\right) & \frac{2\sqrt 3}{3} & \left(\frac{2\sqrt 3}{3} ,2\right) \\ \hline
f'\left(x\right) & + & 0 & - \\ \hline
f\left(x\right) & 单调递增 & 极大值 & 单调递减 \\ \hline
\end{array} \]由上表易知，当 $PA = x = \dfrac{2\sqrt 3 }{3}$ 时，有 ${V_{A' -PBCD}}$ 取最大值． -
若点 $ P $ 为 $ AB $ 的中点，$ E $ 为 $A'C$ 的中点，求证：$A'B \perp DE$．标注答案略解析取 $A'B$ 的中点 $ F $，连接 $ EF$，$FP $．
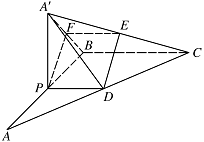由已知得 $ EF \parallel BC \parallel PD , EF= \dfrac{1}{2}BC=PD$，
因此 $ ED\parallel FP$，结合 $\triangle A'PB$ 为等腰直角三角形，知 $A'B \perp PF$，
所以 $A'B \perp DE$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
