如图,$\triangle ABC$ 中,$BA=BC$,延长 $BA$ 至点 $D$ 使 $BD=AC$,若 $\angle BCD=50^\circ$,求证:$\angle B=100^\circ$.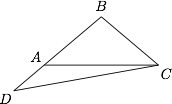

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
设 $BD=AC=2$,$\angle BDC=\theta$,则 $\angle DCA=25^\circ -\dfrac 12\theta$,$\angle BCA=25^\circ+\dfrac12\theta$.在 $\angle ADC$ 中应用正弦定理,可得\[\dfrac{AC}{\sin\angle BDC}=\dfrac{AD}{\sin\angle ACD}=\dfrac{AC-AB}{\sin\angle ACD},\]于是\[\dfrac{2}{\sin\theta}=\dfrac{2-\dfrac{1}{\cos\left(25^\circ+\dfrac 12\theta\right)}}{\sin\left(25^\circ-\dfrac 12\theta\right)},\]即\[2\sin\left(25^\circ-\dfrac 12\theta\right)\cdot \cos\left(25^\circ+\dfrac 12\theta\right)=2\cos\left(25^\circ+\dfrac 12\theta\right)\cdot \sin\theta-\sin\theta,\]积化和差,得\[2\sin\theta\cos\left(25^\circ+\dfrac 12\theta\right)=\sin 50^\circ.\]设等式左边函数为 $f(\theta)$,则其导函数\[f'(\theta)=\cos \theta\cdot\cos \left(\dfrac 12\theta+25^\circ\right)\cdot \left[2-\tan \theta\cdot\tan \left(\dfrac 12\theta+25^\circ\right)\right],\]于是当 $\theta$ 在不超过 $50^\circ$ 时,$f(\theta)$ 单调递增,结合 $f(30^\circ)=\sin 50^\circ$,可得 $\theta=30^\circ$,因此 $\angle B=100^\circ$.
答案
解析
备注