已知函数 $f(x)=|x-m|$,$g(x)=x|x-m|+m^2-7m$.
【难度】
【出处】
无
【标注】
-
若关于 $x$ 的方程 $f(x)=|m|$ 在区间 $[-4,+\infty)$ 上有两个不同的实数根,求实数 $m$ 的取值范围;标注答案$[-2,0)\cup(0,+\infty)$解析容易解得方程 $f(x)=|m|$ 的两个根分别为 $x=0$ 和 $x=2m$,其中 $m\ne 0$.于是可得实数 $m$ 的取值范围是 $[-2,0)\cup(0,+\infty)$.
-
若对任意 $x_1\in (-\infty,4]$,均存在 $x_2\in[3,+\infty)$,使得 $f(x_1)>g(x_2)$ 成立,求实数 $m$ 的取值范围.标注答案$\left(1,4+2\sqrt 3\right)$解析根据题意,有\[\min_{x\leqslant 4}f(x)>\min_{x\geqslant 3}g(x).\]而\[\min_{x\leqslant 4}f(x)=\begin{cases}f(m),&m\leqslant 4,\\ f(4), &m>4,\end{cases}\]即\[\min_{x\leqslant 4}f(x)=\begin{cases}0,&m\leqslant 4,\\ m-4, &m>4,\end{cases}\]而\[\min_{x\geqslant 3}g(x)=\begin{cases}g(3),&m<3,\\ g(m),&m\geqslant 3,\end{cases}\]即\[\min_{x\geqslant 3}g(x)=\begin{cases}m^2-10m+9,&m<3,\\ m^2-7m,&m\geqslant 3.\end{cases}\]如图,画出两个函数的图象,可得 $m$ 的取值范围是 $\left(1,4+2\sqrt 3\right)$.
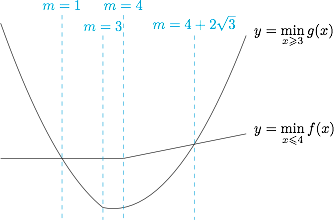
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2