已知 $A,B$ 是椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ 的长轴顶点,$P,Q$ 是椭圆上的两点,且满足 $k_{AP}=\lambda k_{QB}$($\lambda>1$).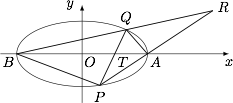

【难度】
【出处】
无
【标注】
-
求证:直线 $AP$ 和 $BQ$ 的交点在定直线上;标注答案略解析根据题意,有\[\begin{split} AP&:y=k_{AP}(x-a),\\ BQ&:y=k_{QB}(x+a),\end{split}\]于是直线 $AP$ 与 $BQ$ 的交点横坐标 $x_0$ 满足\[\dfrac{x_0+a}{x_0-a}=\lambda,\]于是\[x_0=\dfrac{\lambda+1}{\lambda-1}\cdot a.\]因此直线 $AP$ 与 $BQ$ 的交点在定直线 $x=\dfrac{\lambda+1}{\lambda-1}\cdot a$ 上.
-
求证:直线 $PQ$ 过定点;标注答案略解析由椭圆的垂径定理,有\[k_{AQ}\cdot k_{BQ}=-\dfrac{b^2}{a^2},\]于是\[k_{AP}\cdot k_{AQ}=-\dfrac{b^2}{a^2}\cdot \lambda.\]将坐标系原点平移至 $A(a,0)$,则椭圆方程为\[\dfrac{(x'+a)^2}{a^2}+\dfrac{y'^2}{b^2}=1,\]与直线 $P'Q'$ 的方程 $mx'+ny'=1$ 化齐次联立可得\[\dfrac{x'^2}{a^2}+\dfrac {2x'}a\cdot (mx'+ny')+\dfrac{y'^2}{b^2}=0,\]也即\[\dfrac{1}{b^2}y'^2+\dfrac{2n}{a}x'y'+\left(\dfrac{2m}a+\dfrac{1}{a^2}\right)x'^2=0,\]因此\[b^2\cdot \left(\dfrac{2m}a+\dfrac{1}{a^2}\right)=-\dfrac{b^2}{a^2}\cdot \lambda,\]解得\[m=-\dfrac{1+\lambda}{2a}.\]于是直线 $P'Q'$ 恒过点 $T'\left(-\dfrac{2a}{1+\lambda},0\right)$,也即原坐标系下的 $T\left(\dfrac{\lambda-1}{\lambda+1}\cdot a,0\right)$.
-
求 $\triangle PQB$ 和 $\triangle PQA$ 面积之差的最大值.标注答案略解析因为 $|BT|-|AT|=2|OT|$,根据题意得到,所求面积之差为 $\triangle OPQ$ 面积的 $2$ 倍.利用伸缩变换\[\begin{cases} x'=x,\\y'=\dfrac abx,\end{cases} \]将椭圆变为圆 $x'^2+y'^2=a^2$,此时点 $T'$ 的坐标不变,为 $\left(\dfrac {\lambda-1}{\lambda+1}\cdot a,0\right)$,三角形 $OP'Q'$ 面积的两倍等于$$2\cdot\dfrac 12\cdot a^2\sin\angle P'OQ'=a^2\sin\angle P'OQ'.$$考虑过定点 $T'$ 的弦所对的圆心角即可,于是得到其最大值为\[\begin{cases}ab,&\dfrac{\lambda-1}{\lambda+1}\geqslant \dfrac{\sqrt 2}2,\\
2ab\cdot \dfrac{\lambda-1}{\lambda+1}\cdot \sqrt{1-\left(\dfrac{\lambda-1}{\lambda+1}\right)^2},&\dfrac{\lambda-1}{\lambda+1}<\dfrac{\sqrt 2}2,\end{cases}\]也即\[\begin{cases}ab,&\lambda\geqslant 3+2\sqrt 2,\\
4ab\cdot \dfrac{\sqrt{\lambda}\cdot (\lambda -1)}{(\lambda+1)^2},&1<\lambda<3+2\sqrt 2.\end{cases}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3